题目内容
(2011•道外区二模)在等腰△ABC中,AC=BC,∠C=90°,点D为AB的中点,以AC为斜边作直角△APC,连接PD.

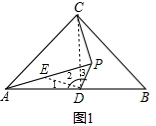
(1)当点P在△ABC的内部时(如图1),求证
PD+PC=AP;
(2)当点P在△ABC的外部时(如图2),线段PD、PC、AP之间的数量关系是
(3)在(2)的条件下,PD与AC的交点为E,连接CD(如图3),PC:EC=7:5,PD=
(AP<PC),求线段PB的长.

(1)当点P在△ABC的内部时(如图1),求证
| 2 |
(2)当点P在△ABC的外部时(如图2),线段PD、PC、AP之间的数量关系是
PA+PC=
PD
| 2 |
PA+PC=
PD
.| 2 |
(3)在(2)的条件下,PD与AC的交点为E,连接CD(如图3),PC:EC=7:5,PD=
7
| ||
| 2 |
分析:(1)通过连接CD,在AP上取一点E使AE=CP,利用等腰三角形的性质证明三角形全等可以得出∠1=∠3,DE=DP,可以得到△EDP是等腰直角三角形.从而得出结论.
(2)连接CD,延长PA到G,使AG=PC,连接DG,由等腰直角三角形的性质可以得到∠ADC=90°,从而可以得到A、P、C、D
四点在以AC为直径的圆上,由∠1=∠2=45°,∠3=∠4,通过证明△PCD≌△GAD,得出∠1=∠G,PD=GD,从而证明△PGD为等腰直角三角形.从而得出答案.PA+PC=
PD
(3)由(2)的结论可以得出AP+PC=7,通过证明△PAD∽△PEC,利用PC:EC=3:5求出AD,从而求出AC,再利用△PEC∽△AED求出PC,就可以求出PA,得出PA=PD得出△PAB是直角三角形,利用勾股定理就可以求出PB.
(2)连接CD,延长PA到G,使AG=PC,连接DG,由等腰直角三角形的性质可以得到∠ADC=90°,从而可以得到A、P、C、D
四点在以AC为直径的圆上,由∠1=∠2=45°,∠3=∠4,通过证明△PCD≌△GAD,得出∠1=∠G,PD=GD,从而证明△PGD为等腰直角三角形.从而得出答案.PA+PC=
| 2 |
(3)由(2)的结论可以得出AP+PC=7,通过证明△PAD∽△PEC,利用PC:EC=3:5求出AD,从而求出AC,再利用△PEC∽△AED求出PC,就可以求出PA,得出PA=PD得出△PAB是直角三角形,利用勾股定理就可以求出PB.
解答:解:(1)证明:连接CD,在AP上取一点E使AE=CP,
∵点D为AB的中点,∠ACB=90°,
∴AD=CD,∠CAD=∠ACD=45°,∠ADC=90°,
∴∠CAP+∠ACD+∠DCP=90°,∠CAP+∠ACD+∠PAD=90°,
∴∠CAP+∠ACD+∠DCP=∠CAP+∠ACD+∠PAD,
∴∠DCP=∠PAD,PC=AE,CD=AD,
∴△CPD≌△AED,
∴DE=DP,∠1=∠3.
∵∠1+∠2=90°,
∴∠3+∠2=90°,
∴△EDP为等腰直角三角形,由勾股定理,得
PE=
PD.
∵AE+EP=AP,
∴PC+
PD=AP.
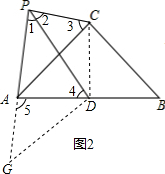
(2)线段PD、PC、AP之间的数量关系是:PA+PC=
PD
证明:连接CD,延长PA到G,使AG=PC,连接DG
∵∠APC=∠ADC=90°,
∴A、D、C、P四点在以AC为直径的圆上.
∵AD=CD,
∴∠1=∠2=45°,
∴∠1=∠2=∠CAD=∠ACD=45°.
∵∠5=∠1+∠4,∠PCD=∠3+∠ACD,∠3=∠4,
∴∠5=∠PCD,PC=AG,AD=CD,
∴△GAD≌△PCD,
∴GD=PD,
∴∠1=∠G=45°,
∴∠PDG=90°,由勾股定理,得
PG=
PD
∵PG=PA+AG,
∴PG=PA+PC,
∴PA+PC=
PD.
(3)∵PD=
∴PA+PC=7.
∵PC:EC=7:5,则设PC=7m,EC=5m,
∴PA=7-7m.
∵△PAD∽△PEC,
∴
=
,
∴
=
,
解得AD=
,在Rt△ADC中,由勾股定理,得
AC=5,
∴在Rt△CAP中,由勾股定理,得
(7m)2+(7-7m)2=25,
解得,m1=
,m2=
.
∵AP<PC,
∴m=
,
∴PC=4,PA=3.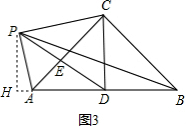
作PH⊥AD于点H,有△PHD∽△APC
∴
=
,
∴
=
解得:PH=
.
在Rt△PHD中,由勾股定理,得
(
)2+HD2=(
)2,
解得:HD=
,HB=
,
在Rt△PHB中由勾股定理,得
PB2=PH2+HB2,
∴PB2=(
)2+(
)2,
解得:PB=
.
∵点D为AB的中点,∠ACB=90°,
∴AD=CD,∠CAD=∠ACD=45°,∠ADC=90°,
∴∠CAP+∠ACD+∠DCP=90°,∠CAP+∠ACD+∠PAD=90°,
∴∠CAP+∠ACD+∠DCP=∠CAP+∠ACD+∠PAD,
∴∠DCP=∠PAD,PC=AE,CD=AD,
∴△CPD≌△AED,
∴DE=DP,∠1=∠3.
∵∠1+∠2=90°,
∴∠3+∠2=90°,
∴△EDP为等腰直角三角形,由勾股定理,得
PE=
| 2 |
∵AE+EP=AP,
∴PC+
| 2 |

(2)线段PD、PC、AP之间的数量关系是:PA+PC=
| 2 |
证明:连接CD,延长PA到G,使AG=PC,连接DG
∵∠APC=∠ADC=90°,
∴A、D、C、P四点在以AC为直径的圆上.
∵AD=CD,
∴∠1=∠2=45°,
∴∠1=∠2=∠CAD=∠ACD=45°.
∵∠5=∠1+∠4,∠PCD=∠3+∠ACD,∠3=∠4,
∴∠5=∠PCD,PC=AG,AD=CD,
∴△GAD≌△PCD,
∴GD=PD,
∴∠1=∠G=45°,
∴∠PDG=90°,由勾股定理,得
PG=
| 2 |
∵PG=PA+AG,
∴PG=PA+PC,
∴PA+PC=
| 2 |

(3)∵PD=
7
| ||
| 2 |
∴PA+PC=7.
∵PC:EC=7:5,则设PC=7m,EC=5m,
∴PA=7-7m.
∵△PAD∽△PEC,
∴
| AD |
| EC |
| PD |
| 3m |
∴
| AD |
| 5m |
| ||||
| 7m |
解得AD=
5
| ||
| 2 |
AC=5,
∴在Rt△CAP中,由勾股定理,得
(7m)2+(7-7m)2=25,
解得,m1=
| 4 |
| 7 |
| 3 |
| 7 |
∵AP<PC,
∴m=
| 4 |
| 7 |
∴PC=4,PA=3.

作PH⊥AD于点H,有△PHD∽△APC
∴
| PH |
| PA |
| PD |
| AC |
∴
| PH |
| 3 |
| ||||
| 5 |
解得:PH=
21
| ||
| 10 |
在Rt△PHD中,由勾股定理,得
(
21
| ||
| 10 |
7
| ||
| 2 |
解得:HD=
14
| ||
| 5 |
81
| ||
| 10 |
在Rt△PHB中由勾股定理,得
PB2=PH2+HB2,
∴PB2=(
21
| ||
| 10 |
81
| ||
| 10 |
解得:PB=
| 65 |
点评:本题考查了相似三角形的判定与性质,全等三角形的判定与性质,等腰直角三角形的性质及勾股定理的运用.

练习册系列答案
相关题目
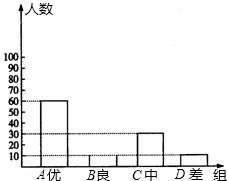 回答下列问题.
回答下列问题.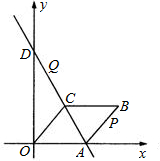 秒
秒