题目内容
【题目】在平面直角坐标系xOy中,对于双曲线y= ![]() (m>0)和双曲线y=
(m>0)和双曲线y= ![]() (n>0),如果m=2n,则称双曲线y=
(n>0),如果m=2n,则称双曲线y= ![]() (m>0)和双曲线y=
(m>0)和双曲线y= ![]() (n>0)为“倍半双曲线”,双曲线y=
(n>0)为“倍半双曲线”,双曲线y= ![]() (m>0)是双曲线y=
(m>0)是双曲线y= ![]() (n>0)的“倍双曲线”,双曲线y=
(n>0)的“倍双曲线”,双曲线y= ![]() (n>0)是双曲线y=
(n>0)是双曲线y= ![]() (m>0)的“半双曲线”,
(m>0)的“半双曲线”,
(1)请你写出双曲线y= ![]() 的“倍双曲线”是;双曲线y=
的“倍双曲线”是;双曲线y= ![]() 的“半双曲线”是;
的“半双曲线”是;
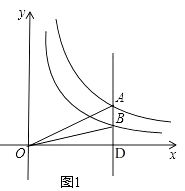
(2)如图1,在平面直角坐标系xOy中,已知点A是双曲线y= ![]() 在第一象限内任意一点,过点A与y轴平行的直线交双曲线y=
在第一象限内任意一点,过点A与y轴平行的直线交双曲线y= ![]() 的“半双曲线”于点B,求△AOB的面积;
的“半双曲线”于点B,求△AOB的面积;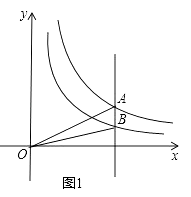
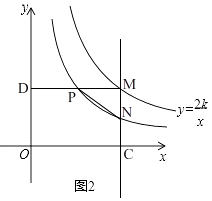
(3)如图2,已知点M是双曲线y= ![]() (k>0)在第一象限内任意一点,过点M与y轴平行的直线交双曲线y=
(k>0)在第一象限内任意一点,过点M与y轴平行的直线交双曲线y= ![]() 的“半双曲线”于点N,过点M与x轴平行的直线交双曲线y=
的“半双曲线”于点N,过点M与x轴平行的直线交双曲线y= ![]() 的“半双曲线”于点P,若△MNP的面积记为S△MNP , 且1≤S△MNP≤2,求k的取值范围.
的“半双曲线”于点P,若△MNP的面积记为S△MNP , 且1≤S△MNP≤2,求k的取值范围.
【答案】
(1)y= ![]() ;y=
;y= ![]()
(2)
解:如图1,
∵双曲线y= ![]() 的“半双曲线”是y=
的“半双曲线”是y= ![]() ,
,
∴△AOD的面积为2,△BOD的面积为1,
∴△AOB的面积为1
(3)
解:解法一:如图2,
依题意可知双曲线 ![]() 的“半双曲线”为
的“半双曲线”为 ![]() ,
,
设点M的横坐标为m,则点M坐标为(m, ![]() ),点N坐标为(m,
),点N坐标为(m, ![]() ),
),
∴CM= ![]() ,CN=
,CN= ![]() .
.
∴MN= ![]() ﹣
﹣ ![]() =
= ![]() .
.
同理PM=m﹣ ![]() =
= ![]() .
.
∴S△PMN= ![]() MNPM=
MNPM= ![]()
∵1≤S△PMN≤2,
∴1≤ ![]() ≤2.
≤2.
∴4≤k≤8,
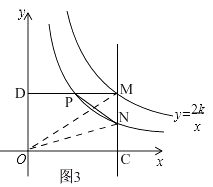
解法二:如图3,
依题意可知双曲线 ![]() 的“半双曲线”为
的“半双曲线”为 ![]() ,
,
设点M的横坐标为m,则点M坐标为(m, ![]() ),点N坐标为(m,
),点N坐标为(m, ![]()
∴点N为MC的中点,同理点P为MD的中点.
连接OM,
∵ ![]() ,
,
∴△PMN∽△OCM.
∴ ![]() .
.
∵S△OCM=k,
∴S△PMN= ![]() .
.
∵1≤S△PMN≤2,
∴1≤ ![]() ≤2.
≤2.
∴4≤k≤8.
【解析】解:(1)由“倍双曲线”的定义
∴双曲线y= ![]() ,的“倍双曲线”是y=
,的“倍双曲线”是y= ![]() ;
;
双曲线y= ![]() 的“半双曲线”是y=
的“半双曲线”是y= ![]() .
.
所以答案是y= ![]() ,y=
,y= ![]() ;
;
【考点精析】掌握反比例函数的概念和反比例函数的图象是解答本题的根本,需要知道形如y=k/x(k为常数,k≠0)的函数称为反比例函数.自变量x的取值范围是x不等于0的一切实数,函数的取值范围也是一切非零实数;反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点.