题目内容
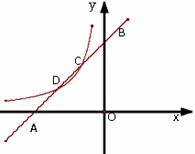
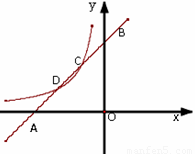
如图,已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,与双曲线
,与双曲线![]()
![]() 分别交于点
分别交于点![]() ,且
,且![]() 点的坐标为
点的坐标为![]() .
.
(1)分别求出直线![]() 及双曲线的解析式;
及双曲线的解析式;
(2)求出点![]() 的坐标;
的坐标;
(3)利用图象直接写出:当![]() 在什么范围内取值时,
在什么范围内取值时,![]() >
>![]() .
.
(1)![]() ,
,![]() ;(2)D(-2,1);(3)
;(2)D(-2,1);(3)![]()
【解析】
试题分析:(1)由点C(-1,2)在直线![]() 及双曲线上即可根据待定系数法求解即可;
及双曲线上即可根据待定系数法求解即可;
(2)把(1)中求得的两个解析式组成方程组求解即可;
(3)找到一次函数的图象在反比例函数的的图象上方的部分对应的x值的取值范围即可得到结果.
解:(1)∵C(-1,2)在双曲线![]() 上,
上,
∴k=-2 ,即双曲线解析式为![]()
∵C(-1,2)在直线![]() 上,
上,
∴2=-1+m,m=3
∴直线解析式为![]() ;
;
(2)由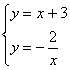 解得
解得![]() 或
或![]()
∴点D(-2,1);
(3)当![]() 时,
时,![]() >
>![]() .
.

练习册系列答案
相关题目
 与
与 轴、
轴、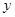 轴分别交于点A、B,与双曲线
轴分别交于点A、B,与双曲线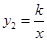 (
( ,2).
,2).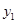 >
>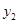 .
.
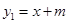 与
与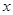 轴、
轴、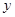 轴分别交于点
轴分别交于点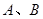 ,与双曲线
,与双曲线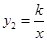
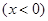 分别交于点
分别交于点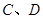 ,且
,且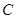 点的坐标为
点的坐标为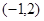 .
.
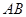 及双曲线的解析式;
及双曲线的解析式;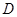 的坐标;
的坐标;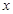 在什么范围内取值时,
在什么范围内取值时,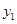 >
>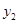 .
.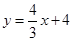 与
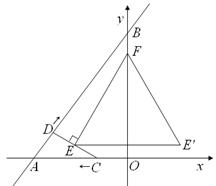
与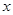 轴,
轴,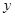 轴分别相交于点
轴分别相交于点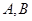 .点
.点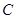 从点
从点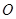 出发沿射线
出发沿射线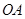 以每秒1个单位长的速度匀速运动,同时点
以每秒1个单位长的速度匀速运动,同时点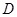 从点
从点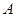 出发沿
出发沿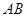 以每秒1个单位长的速度向点
以每秒1个单位长的速度向点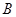 匀速运动.当点
匀速运动.当点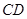 ,
,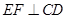 交
交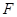 .记
.记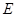 关于
关于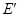 .设点
.设点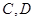 运动的时间是秒(
运动的时间是秒(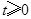 ).
).
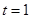 时,则
时,则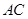 = ,点
= ,点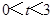 时,若记四边形BDCO的面积为S,则求S关于的函数解析式
时,若记四边形BDCO的面积为S,则求S关于的函数解析式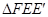 为等腰直角三角形时,请直接写出的值
为等腰直角三角形时,请直接写出的值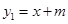 与
与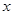 轴、
轴、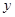 轴分别交于点A、B,与双曲线
轴分别交于点A、B,与双曲线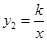 (
(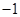 ,2).
,2).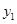 >
>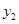 .
.