Question

如图，在矩形ABCD中，AB=6，AD=11．直角尺的直角顶点P在AD上滑动时（点P与A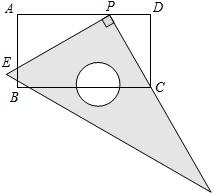，D不重合），一直角边始终经过点C，另一直角边与AB交于点E．
（1）△CDP与△PAE相似吗？如果相似，请写出证明过程；
（2）当∠PCD=30°时，求AE的长；
（3）是否存在这样的点P，使△CDP的周长等于△PAE周长的2倍？若存在，求DP的长；若不存在，请说明理由．

Answer 1

（1）△CDP∽△PAE．（1分）
证明：∵四边形ABCD是矩形，
∴∠D=∠A=90°，CD=AB=6，（2分）
∴∠PCD+∠DPC=90°，（3分）
又∵∠CPE=90°，
∴∠EPA+∠DPC=90°，（4分）
∴∠PCD=∠EPA，（5分）
∴△CDP∽△PAE．（6分）

（2）在Rt△PCD中，由tan∠PCD=

PD

CD

，（7分）
∴PD=CD•tan∠PCD=6•tan30°=6×

3

3

=2

3

，（8分）
∴AP=AD-PD=11-2

3

，（9分）
解法1：由△CDP∽△PAE知：

PD

AE

=

CD

AP

，
∴AE=

PD•AP

CD

=

2 3 ×(11-2 3 )

6

=

11

3

3

-2，（10分）
解法2：由△CDP∽△PAE知：∠EPA=∠PCD=30°，
∴AE=AP•tan∠EAP=(11-2

3)

•tan30°=

11

3

3

-2；（10分）

（3）假设存在满足条件的点P，设DP=x，则AP=11-x，
∵△CDP∽△PAE，
根据△CDP的周长等于△PAE周长的2倍，得到两三角形的相似比为2，
∴

CD

AP

=2即

6

11-x

=2，（11分）
解得x=8，
此时AP=3，AE=4．（12分）