题目内容
如图所示,已知直线l的解析式为y=-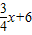 ,并且与x轴、y轴分别交于点A、B.
,并且与x轴、y轴分别交于点A、B.(1)求A、B两点的坐标.
(2)一个半径为1的动圆⊙P (起始时圆心P在原点O处),以4个单位/秒的速度沿x轴正方向运动,问经过多长时间与直线l相切.
(3)若在圆开始运动的同时,一动点Q从B出发,沿BA方向以5个单位/秒的速度运动,在整个运动过程中,问经过多长时间直线PQ经过△AOB的重心M?
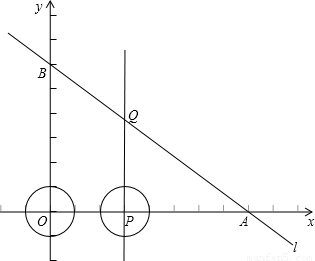
【答案】分析:(1)本题需先根据直线l的解析式与x轴、y轴分别相交,即可得出A、B两点的坐标.
(2)本题需先求出动圆⊙P与直线l相切时移动的距离再除以⊙P运动的速度即可得出结果.
(3)本题需先设运动时间为t,然后得出点P与Q的横坐标相同,再求出△AOB的重心的坐标即可求出4t的值,从而解出t的值.
解答:解:(1)A(8,0)(0,6)
(2)当⊙P运动到P1时,与直线L相切
设切点为D
则P1D=1
∵△ADP1∽△AOB
∴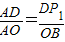
∴
∴AD=
∴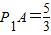
∴OP1=8- =
=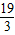
∵动圆⊙P以4个单位/秒的速度沿x轴正方向运动,
∴经过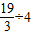 =
=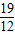 秒与直线l相切.
秒与直线l相切.
当⊙P运动到P2时,则P2A=
∴OP2=8+ =
=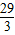
∴经过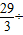 4=
4=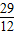 秒与直线l相切.
秒与直线l相切.
(3)设运动时间为t,则
BQ=5t,OP=4t
则点Q的横坐标为4t
∴点P与Q的横坐标相同
∴PQ∥y轴
∵△AOB的重心的坐标为(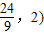
∴PQ过△AOB的重心时
则4t=
t=
∴经过 秒直线PQ经过△AOB的重心M.
秒直线PQ经过△AOB的重心M.
点评:本题主要考查了一次函数的综合应用,在解题时要注意把一次函数的图象和性质与相似三角形相结合是本题的关键.
(2)本题需先求出动圆⊙P与直线l相切时移动的距离再除以⊙P运动的速度即可得出结果.
(3)本题需先设运动时间为t,然后得出点P与Q的横坐标相同,再求出△AOB的重心的坐标即可求出4t的值,从而解出t的值.
解答:解:(1)A(8,0)(0,6)
(2)当⊙P运动到P1时,与直线L相切
设切点为D
则P1D=1
∵△ADP1∽△AOB
∴
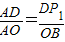
∴

∴AD=

∴
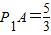
∴OP1=8-
 =
=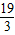
∵动圆⊙P以4个单位/秒的速度沿x轴正方向运动,
∴经过
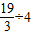 =
=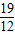 秒与直线l相切.
秒与直线l相切.当⊙P运动到P2时,则P2A=

∴OP2=8+
 =
=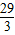
∴经过
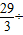 4=
4=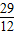 秒与直线l相切.
秒与直线l相切.(3)设运动时间为t,则
BQ=5t,OP=4t
则点Q的横坐标为4t
∴点P与Q的横坐标相同
∴PQ∥y轴
∵△AOB的重心的坐标为(
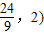
∴PQ过△AOB的重心时
则4t=

t=

∴经过
 秒直线PQ经过△AOB的重心M.
秒直线PQ经过△AOB的重心M.点评:本题主要考查了一次函数的综合应用,在解题时要注意把一次函数的图象和性质与相似三角形相结合是本题的关键.

练习册系列答案
相关题目
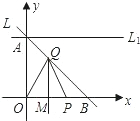 三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.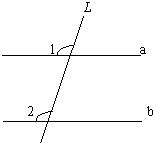 4、如图所示,已知直线a∥b,被直线L所截,如果∠1=69°36′,那么∠2=
4、如图所示,已知直线a∥b,被直线L所截,如果∠1=69°36′,那么∠2=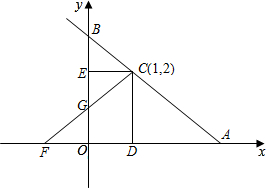 平移,设平移过程中△F′O′G′与四边形ODCE重叠部分面积为y,OO′的长为x(0≤x≤1),求y与x的函数关系式.
平移,设平移过程中△F′O′G′与四边形ODCE重叠部分面积为y,OO′的长为x(0≤x≤1),求y与x的函数关系式.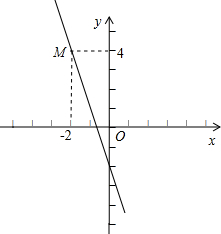 如图所示,已知直线y=kx-2经过M点,求此直线与x轴交点坐标和直线与两坐标轴围成三角形的面积.
如图所示,已知直线y=kx-2经过M点,求此直线与x轴交点坐标和直线与两坐标轴围成三角形的面积. 如图所示:已知直线y=
如图所示:已知直线y=