题目内容
已知一次函数y=kx+1的图象与反比例函数y=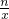 的图象相交于点M(2,3).
的图象相交于点M(2,3).
(1)求这两个函数的关系式;
(2)若两函数图象的另一交点为N,求△OMN(O是坐标原点)的面积.
解:
(1)将M(2,3)代入y=kx+1,得3=2k+1,∴k=1,则一次函数关系式为y=x+1,
将M(2,3)代入y=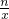 ,得3=
,得3= ,∴n=6,故反比例函数关系式为y=
,∴n=6,故反比例函数关系式为y= .
.
(2)由 得
得 或
或 ,
,
∴N点的坐标为(-3,-2),设直线y=x+1与x轴的交点为A,令y=0得x=-1,
∴A(-1,0),
∴S△OMN=S△OAM+S△OAN= ×1×3+
×1×3+ ×1×2=2.5.
×1×2=2.5.
分析:(1)把M(2,3)代入两个函数解析式即可求解;
(2)让两个函数解析式组成方程组求出另一交点坐标,把△OMN分成被y轴所截得的两个三角形即可.
点评:过某个点,这个点的坐标应适合这个函数解析式.在坐标轴上的三角形的面积通常选用被y轴分割成的两个三角形的面积的和.
(1)将M(2,3)代入y=kx+1,得3=2k+1,∴k=1,则一次函数关系式为y=x+1,
将M(2,3)代入y=
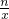 ,得3=
,得3= ,∴n=6,故反比例函数关系式为y=
,∴n=6,故反比例函数关系式为y= .
.(2)由
 得
得 或
或 ,
,∴N点的坐标为(-3,-2),设直线y=x+1与x轴的交点为A,令y=0得x=-1,
∴A(-1,0),
∴S△OMN=S△OAM+S△OAN=
 ×1×3+
×1×3+ ×1×2=2.5.
×1×2=2.5.分析:(1)把M(2,3)代入两个函数解析式即可求解;
(2)让两个函数解析式组成方程组求出另一交点坐标,把△OMN分成被y轴所截得的两个三角形即可.
点评:过某个点,这个点的坐标应适合这个函数解析式.在坐标轴上的三角形的面积通常选用被y轴分割成的两个三角形的面积的和.

练习册系列答案
相关题目
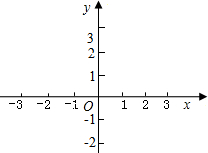 已知一次函数y=kx+2的图象经过A(-1,1).
已知一次函数y=kx+2的图象经过A(-1,1). m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.
m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.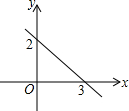 已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.
已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.