题目内容
【题目】正方形网格中的交点，我们称之为格点．如图所示的网格图中，每个小正方形的边长都为
．现有格点
,那么,在网格图中找出格点
,使以和格点为顶点的三角形的面积为
．这样的点可找到的个数为（ ）
A.
B.
C.
D.
【答案】C
【解析】
因为每个小正方形的边长是1，则可以先找到一点C，则三角形ABC的面积是2，满足题目要求，再过C点作AB的平行线，平行线与网格点重合的点，因这些点与A、B组成的三角形都是同底等高，则这些三角形的面积都是2，所以这些点即为符合要求的点；同理，过D点作AB的平行线，与网格点重合的点也是符合要求的格点．将所有的符合要求的格点数加起来，就是问题的答案．
解：如图所示，在网格图中可以找到点C，
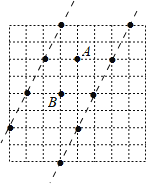
则三角形ABC的面积是2，再过C点作AB的平行线，平行线与网格点重合的点即为符合要求的点，这样的点有5个；
同样的方法，过D点作AB的平行线，又能得到4个不同符合要求的格点，
所以符合要求的格点共有：5+4=9（个）；
故选：C．
练习册系列答案
相关题目
