题目内容
(2012•龙岗区二模)如图1,等腰梯形ABCD中,AD∥BC,AB=CD= ,AD=5,BC=3.以AD所在的直线为x轴,过点B且垂直于AD的直线为y轴建立平面直角坐标系.抛物线y=ax2+bx+c经过O、C、D三点.
,AD=5,BC=3.以AD所在的直线为x轴,过点B且垂直于AD的直线为y轴建立平面直角坐标系.抛物线y=ax2+bx+c经过O、C、D三点.(1)求抛物线的函数表达式;
(2)设(1)中的抛物线与BC交于点E,P是该抛物线对称轴上的一个动点(如图2):
①若直线PC把四边形AOEB的面积分成相等的两部分,求直线PC的函数表达式;
②连接PB、PA,是否存在△PAB是直角三角形?若存在,求出所有符合条件的点P的坐标,并直接写出相应的△PAB的外接圆的面积;若不存在,请说明理由.

【答案】分析:(1)首先过点C作CF⊥AD于F,根据题意可得Rt△AOB≌Rt△CFD,则可得C(3,3),D(4,0),则利用待定系数法即可求得此抛物线的解析式;
(2)①连接AE交OB于点G,因为E的纵坐标为3,代入即可求得其横坐标的值,则可求得BE的长,则可证得四边形AOEB是平行四边形,当PC过点G时,PC把四边形AOEB的面积平分,由点C与G的坐标,利用待定系数法即可求得直线PC的解析式;
②首先求得M与N的坐标,再分别从PB2=PM2+BM2=(y-3)2+4,PA2=PM2+AM2=y2+9,AB2=10这三方面去分析,注意不要漏解,
解答: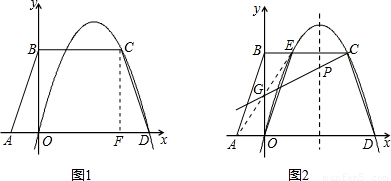 解:(1)过点C作CF⊥AD于F,
解:(1)过点C作CF⊥AD于F,
由已知得:Rt△AOB≌Rt△CFD,OF=BC=3,
∴AO=DF=1,OD=OF+DF=4,
∴CF= ,
,
∴C(3,3),D(4,0),
∴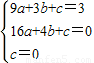 ,
,
解得:a=-1,b=4,c=0,
∴所求的抛物线为y=-x2+4x;
(2)①连接AE交OB于点G,
把y=3代入y=-x2+4x,
得:-x2+4x=3,
解得:x1=1,x2=3,
∴E(1,3),
∴BE=1=OA,
∵BE∥OA,
∴四边形AOEB是平行四边形,
∴当PC过点G(G为AOEB两条对角线的交点)时,PC把四边形AOEB的面积平分,
∵OG= OB=
OB= ,
,
∴G(0, ),
),
∴C(3,3),
∴直线CG为: ,
,
∴即直线PC为: ;
;
②存在满足条件的点P,
由(1)知抛物线的对称轴为x=2,
设P(2,y),对称轴交BC于点M,交x轴于点N,
则M(2,3),N(2,0),
∴PB2=PM2+BM2=(y-3)2+4,PA2=PM2+AM2=y2+9,AB2=10,
有三种可能,
若∠PBA=90°,则PA2=PB2+AB2,
∴y2+9=(y-3)2+4+10,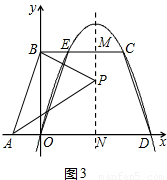
解得y= ,
,
∴P(2, ),
),
∴AP=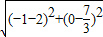 =
= ,
,
此时△PAB外接圆的面积是:π×( ×
×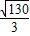 )2=
)2= π,
π,
若∠PAB=90°,则PB2=PA2+AB2,
∴(y-3)2+4=y2+9+10,
解得:y=-1,
∴P(2,-1),
∴BP=2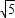 ,
,
此时△PAB外接圆的面积是:5π,
若∠APB=90°,则PB2+PA2=AB2,
∴(y-3)2+4+y2+9=10,此方程无实数根,
∴此时满足条件的点P不存在,
综上所述,存在满足条件的点P,
当点P(2, )时,△PAB外接圆的面积是
)时,△PAB外接圆的面积是 π,
π,
当点P(2,-1)时,△PAB外接圆的面积是5π.
点评:此题考查了待定系数法求函数的解析式,以及平行四边形的判定与性质等知识.此题综合性很强,注意数形结合思想与分类讨论思想的应用.
(2)①连接AE交OB于点G,因为E的纵坐标为3,代入即可求得其横坐标的值,则可求得BE的长,则可证得四边形AOEB是平行四边形,当PC过点G时,PC把四边形AOEB的面积平分,由点C与G的坐标,利用待定系数法即可求得直线PC的解析式;
②首先求得M与N的坐标,再分别从PB2=PM2+BM2=(y-3)2+4,PA2=PM2+AM2=y2+9,AB2=10这三方面去分析,注意不要漏解,
解答:
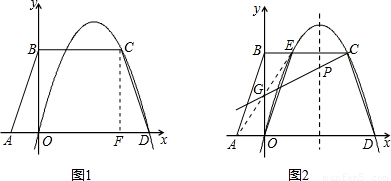 解:(1)过点C作CF⊥AD于F,
解:(1)过点C作CF⊥AD于F,由已知得:Rt△AOB≌Rt△CFD,OF=BC=3,
∴AO=DF=1,OD=OF+DF=4,
∴CF=
 ,
,∴C(3,3),D(4,0),
∴
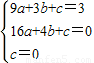 ,
,解得:a=-1,b=4,c=0,
∴所求的抛物线为y=-x2+4x;
(2)①连接AE交OB于点G,
把y=3代入y=-x2+4x,
得:-x2+4x=3,
解得:x1=1,x2=3,
∴E(1,3),
∴BE=1=OA,
∵BE∥OA,
∴四边形AOEB是平行四边形,
∴当PC过点G(G为AOEB两条对角线的交点)时,PC把四边形AOEB的面积平分,
∵OG=
 OB=
OB= ,
,∴G(0,
 ),
),∴C(3,3),
∴直线CG为:
 ,
,∴即直线PC为:
 ;
;②存在满足条件的点P,
由(1)知抛物线的对称轴为x=2,
设P(2,y),对称轴交BC于点M,交x轴于点N,
则M(2,3),N(2,0),
∴PB2=PM2+BM2=(y-3)2+4,PA2=PM2+AM2=y2+9,AB2=10,
有三种可能,
若∠PBA=90°,则PA2=PB2+AB2,
∴y2+9=(y-3)2+4+10,

解得y=
 ,
,∴P(2,
 ),
),∴AP=
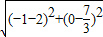 =
= ,
,此时△PAB外接圆的面积是:π×(
 ×
×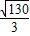 )2=
)2= π,
π,若∠PAB=90°,则PB2=PA2+AB2,
∴(y-3)2+4=y2+9+10,
解得:y=-1,
∴P(2,-1),
∴BP=2
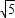 ,
,此时△PAB外接圆的面积是:5π,
若∠APB=90°,则PB2+PA2=AB2,
∴(y-3)2+4+y2+9=10,此方程无实数根,
∴此时满足条件的点P不存在,
综上所述,存在满足条件的点P,
当点P(2,
 )时,△PAB外接圆的面积是
)时,△PAB外接圆的面积是 π,
π,当点P(2,-1)时,△PAB外接圆的面积是5π.
点评:此题考查了待定系数法求函数的解析式,以及平行四边形的判定与性质等知识.此题综合性很强,注意数形结合思想与分类讨论思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 上的一点,⊙M与y轴切于点C,与x轴交于A、B两点.若点C的坐标为(0,2),点A的坐标为(1,0),则k的值为 .
上的一点,⊙M与y轴切于点C,与x轴交于A、B两点.若点C的坐标为(0,2),点A的坐标为(1,0),则k的值为 .

 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.