题目内容
(2012•龙岗区二模)如图,菱形ABCD中,过点C作CE⊥AB,交AB的延长线于点E,作CF⊥AD,交AD的延长线于点F.(1)求证:△CBE≌△CDF;
(2)若∠CAE=30°,CE=3,求菱形ABCD的面积.

【答案】分析:(1)本题需根据菱形的性质和直角三角形全等的判定方法即可证出结论.
(2)本题需利用解直角三角形求出菱形的边长,再根据菱形的面积公式即可求出结果.
解答: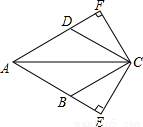 (1)证明:∵四边形ABCD是菱形,
(1)证明:∵四边形ABCD是菱形,
∴BC=CD,∠ABC=∠ADC,
∵∠ABC+∠CBE=180°,∠ADC+∠CDF=180°,
∴∠CBE=∠CDF,
∵CE⊥AB,CF⊥AD,
∴∠CEB=∠CFD=90°,
∴△CBE≌△CDF;
(2)解:∵四边形ABCD是菱形,
∴∠BAD=2∠CAE=60°,BC∥AD,
∴∠CBE=∠BAD=60°,
∵sin∠CBE=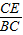 ,
,
∴BC=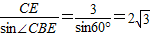 ,
,
∴S菱形ABCD=AB×CE=BC×CE=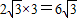 .
.
点评:本题主要考查了菱形的性质,解题时要注意解直角三角形和三角形全等的判定的综合应用.
(2)本题需利用解直角三角形求出菱形的边长,再根据菱形的面积公式即可求出结果.
解答:
 (1)证明:∵四边形ABCD是菱形,
(1)证明:∵四边形ABCD是菱形,∴BC=CD,∠ABC=∠ADC,
∵∠ABC+∠CBE=180°,∠ADC+∠CDF=180°,
∴∠CBE=∠CDF,
∵CE⊥AB,CF⊥AD,
∴∠CEB=∠CFD=90°,
∴△CBE≌△CDF;
(2)解:∵四边形ABCD是菱形,
∴∠BAD=2∠CAE=60°,BC∥AD,
∴∠CBE=∠BAD=60°,
∵sin∠CBE=
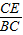 ,
,∴BC=
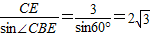 ,
,∴S菱形ABCD=AB×CE=BC×CE=
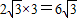 .
.点评:本题主要考查了菱形的性质,解题时要注意解直角三角形和三角形全等的判定的综合应用.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
 ,AD=5,BC=3.以AD所在的直线为x轴,过点B且垂直于AD的直线为y轴建立平面直角坐标系.抛物线y=ax2+bx+c经过O、C、D三点.
,AD=5,BC=3.以AD所在的直线为x轴,过点B且垂直于AD的直线为y轴建立平面直角坐标系.抛物线y=ax2+bx+c经过O、C、D三点.
 上的一点,⊙M与y轴切于点C,与x轴交于A、B两点.若点C的坐标为(0,2),点A的坐标为(1,0),则k的值为 .
上的一点,⊙M与y轴切于点C,与x轴交于A、B两点.若点C的坐标为(0,2),点A的坐标为(1,0),则k的值为 .
 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.