题目内容
(2012•龙岗区二模)如图,平面直角坐标系中,M是双曲线y= 上的一点,⊙M与y轴切于点C,与x轴交于A、B两点.若点C的坐标为(0,2),点A的坐标为(1,0),则k的值为 .
上的一点,⊙M与y轴切于点C,与x轴交于A、B两点.若点C的坐标为(0,2),点A的坐标为(1,0),则k的值为 .
【答案】分析:连接CM,AM,过点M作MD⊥AB,在直角三角形ADM中,由勾股定理得出⊙M的半径为r,从而得出点M的坐标,即可得出答案.
解答: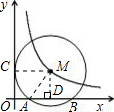 解:如图,连接CM,AM,过点M作MD⊥AB,垂足为D,
解:如图,连接CM,AM,过点M作MD⊥AB,垂足为D,
设⊙M的半径为r,在直角三角形ADM中,
由勾股定理得AM2=AD2+DM2,
即r2=(r-1)2+22,
解得r=2.5,
∴点M的坐标(2.5,2)
∴反比例函数的解析式为y=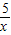 .
.
故答案为:5.
点评:本题是一道反比例函数的综合题目,考查了用待定系数法求反比例函数的解析式以及勾股定理.
解答:
 解:如图,连接CM,AM,过点M作MD⊥AB,垂足为D,
解:如图,连接CM,AM,过点M作MD⊥AB,垂足为D,设⊙M的半径为r,在直角三角形ADM中,
由勾股定理得AM2=AD2+DM2,
即r2=(r-1)2+22,
解得r=2.5,
∴点M的坐标(2.5,2)
∴反比例函数的解析式为y=
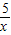 .
.故答案为:5.
点评:本题是一道反比例函数的综合题目,考查了用待定系数法求反比例函数的解析式以及勾股定理.

练习册系列答案
相关题目
 ,AD=5,BC=3.以AD所在的直线为x轴,过点B且垂直于AD的直线为y轴建立平面直角坐标系.抛物线y=ax2+bx+c经过O、C、D三点.
,AD=5,BC=3.以AD所在的直线为x轴,过点B且垂直于AD的直线为y轴建立平面直角坐标系.抛物线y=ax2+bx+c经过O、C、D三点.

 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.