题目内容
在我市开展的“南国书香伴我行”读书活动中,某中学为了解九年级300名学生读书情况,随机调查了九年级50名学生读书的册数.统计数据如下表所示:
| 册数 | 0 | 1 | 2 | 3 | 4 |
| 人数 | 1 | 13 | 16 | 17 | 3 |
(2)根据样本数据,估计该校八年级300名学生在本次活动中读书多于2册的人数;
(3)学校广播站的小记者对被调查的50名学生中读书册数最少或最多的人进行采访,请利用树状图或列表,求被采访的两人恰好都是读书册数最多的学生的概率.
解:(1)读3册的人数最多为17人,
所以,众数为3,
按照读书册数的多少从小到大的顺序排列,第25、26人都是读了2册,
所以,中位数为2;
(2)在50名学生中,读书多于2本的学生有20名,
所以,300× =120,
=120,
答:根据样本数据,可以估计该校八年级300名学生在本次活动中读书多于2册的约有120名;
(3)设读书最少的人为A,读书最多的人为B1,B2,B3,
所以,被采访的两人恰好都是读书册数最多的学生的情况如下:(B1,B2)、(B1,B3)、(B2,B1)、(B2,B3)、(B3,B1)、(B3,B2),共6种,
所以,被采访的两人恰好都是读书册数最多的学生的概率为P=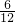 =
= .
.
故答案为:3;2.
分析:(1)根据众数的定义,找出出现次数最多的册数即为众数,按照从小到大的顺序排列,找出第25、26两个数,然后求平均数即为这组数的中位数;
(2)用多余2册的人数所占的份数乘以总人数300,计算即可得解;
(3)设读书最少的人为A,读书最多的人为B1,B2,B3,列出表格,然后根据概率公式列式计算即可得解.
点评:本题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.
所以,众数为3,
按照读书册数的多少从小到大的顺序排列,第25、26人都是读了2册,
所以,中位数为2;
(2)在50名学生中,读书多于2本的学生有20名,
所以,300×
 =120,
=120,答:根据样本数据,可以估计该校八年级300名学生在本次活动中读书多于2册的约有120名;
(3)设读书最少的人为A,读书最多的人为B1,B2,B3,
| A | B1 | B2 | B3 | |
| A | (A,B1) | (A,B2) | (A,B3) | |
| B1 | (B1,A) | (B1,B2) | (B1,B3) | |
| B2 | (B2,A) | (B2,B1) | (B2,B3) | |
| B3 | (B3,A) | (B3,B1) | (B3,B2) |
所以,被采访的两人恰好都是读书册数最多的学生的概率为P=
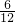 =
= .
.故答案为:3;2.
分析:(1)根据众数的定义,找出出现次数最多的册数即为众数,按照从小到大的顺序排列,找出第25、26两个数,然后求平均数即为这组数的中位数;
(2)用多余2册的人数所占的份数乘以总人数300,计算即可得解;
(3)设读书最少的人为A,读书最多的人为B1,B2,B3,列出表格,然后根据概率公式列式计算即可得解.
点评:本题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
在我市开展的“南国书香伴我行”读书活动中,某中学为了解九年级300名学生读书情况,随机调查了九年级50名学生读书的册数.统计数据如下表所示:
(1)这50个样本数据的众数是______,中位数是______;
(2)根据样本数据,估计该校八年级300名学生在本次活动中读书多于2册的人数;
(3)学校广播站的小记者对被调查的50名学生中读书册数最少或最多的人进行采访,请利用树状图或列表,求被采访的两人恰好都是读书册数最多的学生的概率.
| 册数 | 1 | 2 | 3 | 4 | |
| 人数 | 1 | 13 | 16 | 17 | 3 |
(2)根据样本数据,估计该校八年级300名学生在本次活动中读书多于2册的人数;
(3)学校广播站的小记者对被调查的50名学生中读书册数最少或最多的人进行采访,请利用树状图或列表,求被采访的两人恰好都是读书册数最多的学生的概率.

 年级50名学生一周内用于阅读课外书籍的时间,有关数据如下面统计图所示.
年级50名学生一周内用于阅读课外书籍的时间,有关数据如下面统计图所示.