题目内容
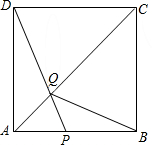 如图,在边长为6的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q,连接BQ.
如图,在边长为6的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q,连接BQ.(1)试证明:无论点P运动到AB上何处时,都有△ADQ≌△ABQ;
(2)当△ADQ的面积与正方形ABCD面积之比为1:6时,求BQ的长度,并直接写出此时点P在AB上的位置.
分析:(1)根据正方形的四条边都相等,对角线平分一组对角,可得AB=AD,∠DAQ=∠BAQ,而AQ是△ADQ和△ABQ的公共边,所以两三角形全等;
(2)根据面积之比为1:6,先求出△ADQ的面积为6,过点Q作QE⊥AD于E,QF⊥AB于F,即可求出AD边上的高QE的长度为2,所以QF也等于2,再求出BF的长度为4,利用勾股定理即可求出BQ的长度,在△DAP中利用相似三角形对应边成比例即可求出AP的长度为3,所以,点P在AB的中点位置.
(2)根据面积之比为1:6,先求出△ADQ的面积为6,过点Q作QE⊥AD于E,QF⊥AB于F,即可求出AD边上的高QE的长度为2,所以QF也等于2,再求出BF的长度为4,利用勾股定理即可求出BQ的长度,在△DAP中利用相似三角形对应边成比例即可求出AP的长度为3,所以,点P在AB的中点位置.
解答:(1)证明:在△ADQ和△ABQ中,
,
∴△ADQ≌△ABQ(SAS);
(2)解:∵△ADQ的面积与正方形ABCD面积之比为1:6,正方形面积为62=36,
∴△ADQ的面积为6,
过点Q作QE⊥AD于E,QF⊥AB于F,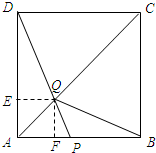
∵△ADQ≌△ABQ,
∴QE=QF,
∴
AD•QE=6,
∴QE=QF=2,
∵∠BAD=∠QEA=∠QFA=90°,
∴四边形AEQF为正方形,
∴AF=QE=2,
∴BF=6-2=4,
在Rt△QBF中,
BQ=
=
=2
,
∵△DEQ∽△DAP,
∴
=
,即
=
,
∴AP=3,
∴P在AB的中点位置(或者回答此时AP=3).
|
∴△ADQ≌△ABQ(SAS);
(2)解:∵△ADQ的面积与正方形ABCD面积之比为1:6,正方形面积为62=36,
∴△ADQ的面积为6,
过点Q作QE⊥AD于E,QF⊥AB于F,

∵△ADQ≌△ABQ,
∴QE=QF,
∴
| 1 |
| 2 |
∴QE=QF=2,
∵∠BAD=∠QEA=∠QFA=90°,
∴四边形AEQF为正方形,
∴AF=QE=2,
∴BF=6-2=4,
在Rt△QBF中,
BQ=
| QF2+BF2 |
| 22+42 |
| 5 |
∵△DEQ∽△DAP,
∴
| DE |
| AD |
| EQ |
| AP |
| 6-2 |
| 6 |
| 2 |
| AP |
∴AP=3,
∴P在AB的中点位置(或者回答此时AP=3).
点评:本题综合考查了正方形的边与角平分线的性质,三角形全等的判定,勾股定理的运用以及平行线分线段成比例定理,对同学们能力要求较高.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
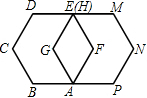 如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点
如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点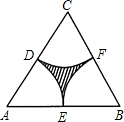 已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
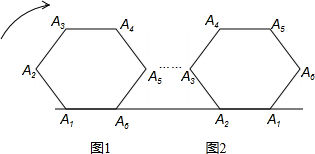 如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )
如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )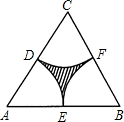 已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
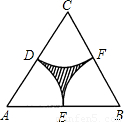
已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,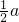 长为半径作
长为半径作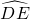 ,
, ,
,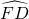 ,求阴影部分的面积.
,求阴影部分的面积.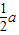 长为半径作
长为半径作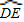 ,
,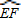 ,
,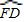 ,求阴影部分的面积.
,求阴影部分的面积.