题目内容
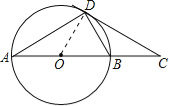
【题目】如图,AB是⊙O的直径,CD是⊙O的切线,切点为D,CD与AB的延长线交于点C,∠A=30°,给出下面3个结论:①AD=CD;②BD=BC;③AB=2BC,其中正确结论的个数( )

A. 3 B. 2 C. 1 D. 0
【答案】A
【解析】试题分析:连接OD,CD是⊙O的切线,可得CD⊥OD,由∠A=30°,可以得出∠ABD=60°,△ODB是等边三角形,∠C=∠BDC=30°,再结合在直角三角形中300所对的直角边等于斜边的一半,继而得到结论①②③成立.
解:如图,连接OD,
∵CD是⊙O的切线,
∴CD⊥OD,
∴∠ODC=90°,
又∵∠A=30°,
∴∠ABD=60°,
∴△OBD是等边三角形,
∴∠DOB=∠ABD=60°,AB=2OB=2OD=2BD.
∴∠C=∠BDC=30°,
∴BD=BC,②成立;
∴AB=2BC,③成立;
∴∠A=∠C,
∴DA=DC,①成立;
综上所述,①②③均成立,
故答案选:A.

练习册系列答案
相关题目


