题目内容
 (2012•成都模拟)设函数y=x2-(2k+1)x+2k-4的图象如图所示,它与x轴交于A,B两点,且线段OA与OB的长度之比为1:3,则k=
(2012•成都模拟)设函数y=x2-(2k+1)x+2k-4的图象如图所示,它与x轴交于A,B两点,且线段OA与OB的长度之比为1:3,则k=| 1 |
| 2 |
| 1 |
| 2 |
分析:令函数解析式中y=0,得到关于x的一元二次方程,设A(a,0),B(b,0),可得出OA=-a,OB=b,可得出一元二次方程的两个解为a与b,利用根与系数的关系表示出a+b与ab,由OA与OB的比值,得到b=-3a,代入表示出的a+b鱼ab中计算,然后消去a得到关于k的方程,求出方程的解即可得到k的值.
解答:解:y=x2-(2k+1)x+2k-4,令y=0,得到x2-(2k+1)x+2k-4=0,
设A(a,0),B(b,0),
可得x2-(2k+1)x+2k-4=0的两个解分别为a,b(a<0,b>0),
则有a+b=2k+1,ab=2k-4,
又线段OA与OB的长度之比为1:3,即-a:b=1:3,
∴b=-3a,
∴a-3a=2k+1,a•(-3a)=2k-4,即a=-
(2k+1)=-k-
①,-3a2=2k-4②,
①代入②消去a得:-3(-k-
)2=2k-4,即12k2+20k-13=0,
分解因式得:(2k-1)(6k+13)=0,
解得:k=
或k=-
,
∵抛物线开口向上,且对称轴在y轴右边,
∴-(2k+1)<0,即k>-
,故k=-
舍去,
∴k=
.
故答案为:
设A(a,0),B(b,0),
可得x2-(2k+1)x+2k-4=0的两个解分别为a,b(a<0,b>0),
则有a+b=2k+1,ab=2k-4,
又线段OA与OB的长度之比为1:3,即-a:b=1:3,
∴b=-3a,
∴a-3a=2k+1,a•(-3a)=2k-4,即a=-
| 1 |
| 2 |
| 1 |
| 2 |
①代入②消去a得:-3(-k-
| 1 |
| 2 |
分解因式得:(2k-1)(6k+13)=0,
解得:k=
| 1 |
| 2 |
| 13 |
| 6 |
∵抛物线开口向上,且对称轴在y轴右边,
∴-(2k+1)<0,即k>-
| 1 |
| 2 |
| 13 |
| 6 |
∴k=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:此题考查了抛物线与x轴的交点,根与系数的关系,以及二次函数的性质,利用了数形结合及消元的数学思想,数形结合思想是数学中重要的解题思想,学生做题时要灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
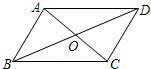 (2012•成都模拟)如图,已知?ABCD的对角线BD=4cm,将?ABCD绕其对称中心O旋转180°,则点D所转过的路径长为( )
(2012•成都模拟)如图,已知?ABCD的对角线BD=4cm,将?ABCD绕其对称中心O旋转180°,则点D所转过的路径长为( )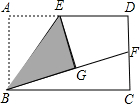 (2012•成都模拟)如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,再延长BG交DC于点F.
(2012•成都模拟)如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,再延长BG交DC于点F.