题目内容
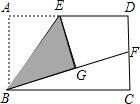（2012•成都模拟）如图，在矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，且点G在矩形ABCD内部，再延长BG交DC于点F．（1）判断GF与DF之长是否相等，并说明理由．
（2）若AD=
| 2 |
| DC |
| DF |
（3）若DC=n?DF，求
| AD |
| AB |
分析：（1）连接EF，由图形翻折变换的性质可知，∠A=∠EGB=90°，AE=EG，由HL定理可得出Rt△EGF≌Rt△EDF，故可得出结论；
（2）由AD=
AB，四边形ABCD是矩形，可知AD=BC=
CD，在Rt△BCF中利用勾股定理即可得出
的值；
（3）GF=DF，设DF=x，BC=y，则有GF=x，AD=y，由DC=n•DF，可知BF=BG+GF=（n+1）x，在Rt△BCF中，由BC2+CF2=BF2即可得出结论．
（2）由AD=
| 2 |
| 2 |
| DC |
| DF |
（3）GF=DF，设DF=x，BC=y，则有GF=x，AD=y，由DC=n•DF，可知BF=BG+GF=（n+1）x，在Rt△BCF中，由BC2+CF2=BF2即可得出结论．
解答：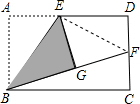
解：（1）连接EF，
∵△BGE由△BAE翻折而成，
∴∠A=∠EGB=90°，AE=EG，
∵E是AD的中点，
∴AE=EG=DE，
∴
，
∴Rt△EGF≌Rt△EDF，
∴GF=DF；
（2）∵AD=
AB，四边形ABCD是矩形，
∴AD=BC=
CD，
在Rt△BCF中，
∵BC2+CF2=BF2，即BC2+（CD-DF）2=（
BC+DF）2，整理得
CD=（2+
）DF，
∴
=
；
（3）∵GF=DF，设DF=x，BC=y，则有GF=x，AD=y
∵DC=n•DF，
∴BF=BG+GF=（n+1）x
在Rt△BCF中，BC2+CF2=BF2，即y2+[（n-1）x]2=[（n+1）x]2
∴y=2x
，
∴
=
=
解：（1）连接EF，∵△BGE由△BAE翻折而成，
∴∠A=∠EGB=90°，AE=EG，
∵E是AD的中点，
∴AE=EG=DE，
∴
|
∴Rt△EGF≌Rt△EDF，
∴GF=DF；
（2）∵AD=
| 2 |
∴AD=BC=
| 2 |
在Rt△BCF中，
∵BC2+CF2=BF2，即BC2+（CD-DF）2=（
| 1 |
| 2 |
| 5 |
| 2 |
| 2 |
∴
| DC |
| DF |
4+2
| ||
| 5 |
（3）∵GF=DF，设DF=x，BC=y，则有GF=x，AD=y
∵DC=n•DF，
∴BF=BG+GF=（n+1）x
在Rt△BCF中，BC2+CF2=BF2，即y2+[（n-1）x]2=[（n+1）x]2
∴y=2x
| n |
∴
| AD |
| AB |
| y |
| nx |
2
| ||
| n |
点评：本题考查的是图形的翻折变换及勾股定理，熟知图形翻折不变性的性质是解答此题的关键．
练习册系列答案
相关题目
（2012•成都模拟）设函数y=x2-（2k+1）x+2k-4的图象如图所示，它与x轴交于A，B两点，且线段OA与OB的长度之比为1：3，则k=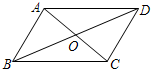
（2012•成都模拟）如图，已知?ABCD的对角线BD=4cm，将?ABCD绕其对称中心O旋转180°，则点D所转过的路径长为（ ）