题目内容
【题目】有如图所示的甲、乙、丙长方形卡片若干张,用它们可以拼一些新的长方形.求长为(a+2b),宽为(2a+b)的长方形面积;若要拼这样一个长方形,则需要甲、乙、丙长方形卡片分别多少张?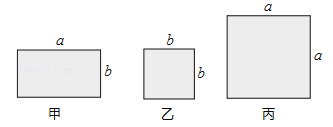
【答案】解:根据题意得:(a+2b)(2a+b)=2a2+ab+4ab+2b2=2a2+5ab+2b2;
∵甲、乙、丙三类卡片的面积分别为ab、b2、a2 ,
∴需要甲、乙、丙长方形卡片分别为5张,2张,2张.
【解析】根据长方形的面积公式求出拼接后的长方形的面积,再利用多项式的乘法运算法则进行计算,然后根据系数即可得解.
【考点精析】关于本题考查的多项式乘多项式,需要了解多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加才能得出正确答案.

练习册系列答案
相关题目
【题目】下列运算正确的是( )
A.(﹣2ab)?(﹣3ab)3=﹣54a4b4
B.5x2?(3x3)2=15x12
C.(﹣0.1 b)?(﹣10b2)3=﹣b7
D.(2×10n)(![]() ×10n)=102n
×10n)=102n
【题目】甲、乙两人在5次打靶测试中命中的环数如下: 甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 | 8 | 0.4 | |
乙 | 9 | 3.2 |
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差 . (填“变大”、“变小”或“不变”).

