ЬтФПФкШн
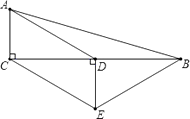
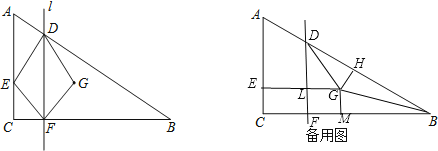
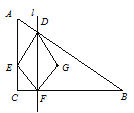
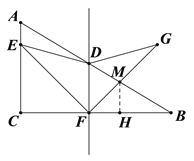
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌЁЯCЃН90ЁуЃЌACЃН3cmЃЌBCЃН4cmЃЌЕуEЁЂFЭЌЪБДгЕуCГіЗЂЃЌвд![]() cm/sЕФЫйЖШЗжБ№биCAЁЂCBдШЫйдЫЖЏЃЌЕБЕуEЕНДяЕу AЪБЃЌСНЕуЭЌЪБЭЃжЙдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊtsЃЎЙ§ЕуFзїBCЕФДЙЯпlНЛABгкЕуDЃЌЕуGгыЕуEЙигкжБЯпlЖдГЦЃЎ
cm/sЕФЫйЖШЗжБ№биCAЁЂCBдШЫйдЫЖЏЃЌЕБЕуEЕНДяЕу AЪБЃЌСНЕуЭЌЪБЭЃжЙдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊtsЃЎЙ§ЕуFзїBCЕФДЙЯпlНЛABгкЕуDЃЌЕуGгыЕуEЙигкжБЯпlЖдГЦЃЎ
ЃЈ1ЃЉЕБt ЃН sЪБЃЌЕуGдкЁЯABCЕФЦНЗжЯпЩЯЃЛ
ЃЈ2ЃЉЕБt ЃН sЪБЃЌЕуGдкABБпЩЯЃЛ
ЃЈ3ЃЉЩшЁїDFGгыЁїDFBжиКЯВПЗжЕФУцЛ§ЮЊScm2ЃЌ ЧѓSгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіtЕФШЁжЕЗЖЮЇЃЎ

ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ2ЃЉ
ЃЈ2ЃЉ![]() ЃЈ3ЃЉЂй
ЃЈ3ЃЉЂй![]() =
= ![]() Ђк
Ђк![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЙ§ЕуGзіGHЁЭBDЃЌДЙзуЮЊHЃЌGMЁЭFBЃЌДЙзуЮЊMЃЌЕуEЁЂFЭЌЪБДгЕуCГіЗЂЃЌЫљвдEC=CF=FM=GM=GH=![]() tЃЌЧвDGвВЪЧЁїBDFЕФНЧЦНЗжЯпЃЌгЩЁїBDFЁзЁїABCЕУЃК
tЃЌЧвDGвВЪЧЁїBDFЕФНЧЦНЗжЯпЃЌгЩЁїBDFЁзЁїABCЕУЃК ![]() ЃЌЁрBDЃН5
ЃЌЁрBDЃН5![]() tЃЌDFЃН3
tЃЌDFЃН3![]() tЃЌПЩЧѓЕУDLЁЂBMЕФГЄЖШЃЌгЩDL=DHЃЌBH=BMЃЌЙЙдьЙигкtЕФЗНГЬПЩвдЧѓЕУД№АИЃЎ
tЃЌПЩЧѓЕУDLЁЂBMЕФГЄЖШЃЌгЩDL=DHЃЌBH=BMЃЌЙЙдьЙигкtЕФЗНГЬПЩвдЧѓЕУД№АИЃЎ
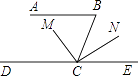
ЃЈ2ЃЉЕуGдкABБпЩЯЪБЃЌЙ§ЕуGзїGHЁЭBCЃЌДЙзуЮЊHЃЌгЩЃЈ1ЃЉжаЕФЪ§жЕЃЌНсКЯЁїBGHЁзЁїBACЃЌЙЙдьГіЙигкtЕФЗНГЬЃЌПЩвдЕУЕНД№АИЃЎ
ЃЈ3ЃЉЃЉгЩDFЁЮACЕУЕНЁїABCЁзЁїDBFЃЌЁр ![]() ЃЌМД
ЃЌМД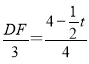 ЃЌЕУЕНDFЃН
ЃЌЕУЕНDFЃН![]() (8t)ЃЌЗжСНжжЧщПіЬжТлЃК
(8t)ЃЌЗжСНжжЧщПіЬжТлЃК
ЂйЕБ0ЃМtЁм![]() ЪБЃЌSЃНSЁїDFGЃНSЁїDEF=
ЪБЃЌSЃНSЁїDFGЃНSЁїDEF=![]() DFCFЃН
DFCFЃН![]() ЁС
ЁС![]() (8t)ЁС
(8t)ЁС![]() t=
t=![]() t2+
t2+![]() tЃЛ
tЃЛ
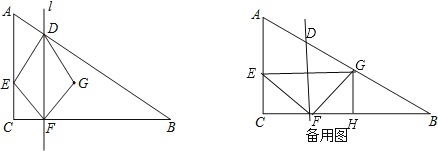
ЂкЕБ![]() ЃМtЁм6ЪБЃЌЩшGНЛABгкЕуMЃЌЙ§ЕуMзїMHЁЭBCгкHЃЌЩшFH=MH=aЃЌЧѓЕУBHЃЌНтГіaгыtЕФЙиЯЕЃЌМЬЖјЧѓЕУSгыtЕФЙиЯЕЃЎ
ЃМtЁм6ЪБЃЌЩшGНЛABгкЕуMЃЌЙ§ЕуMзїMHЁЭBCгкHЃЌЩшFH=MH=aЃЌЧѓЕУBHЃЌНтГіaгыtЕФЙиЯЕЃЌМЬЖјЧѓЕУSгыtЕФЙиЯЕЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉ![]()
ЩшDFЃЌEGЯрНЛгкLЃЌЙ§ЕуGзіGHЁЭBDЃЌДЙзуЮЊHЃЌGMЁЭFBЃЌДЙзуЮЊMЃЌЕуEЁЂFЭЌЪБДгЕуCГіЗЂЃЌЫљвдЫФБпаЮECFLЁЂЫФБпаЮLFGMЖМЪЧе§ЗНаЮЃЌ
ЁрEC=CF=FM=GM=GH=![]() tЃЌ
tЃЌ
гжЁпDGвВЪЧЁїBDFЕФНЧЦНЗжЯпЃЌ
ЁрDL=DHЃЌ
ЁпDFЁЮACЃЌ
ЁрЁїBDFЁзЁїBACЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрBDЃН5![]() tЃЌDFЃН3
tЃЌDFЃН3![]() tЃЌ
tЃЌ
гжЁпDL=DH=3![]() t
t![]() tЃН3
tЃН3![]() tЃЌ
tЃЌ
BH=BM=4-tЃЌгжЁпBD=BH+HDЃЌ
Ёр5![]() tЃН3
tЃН3![]() t+4tЃЌНтЕУЃКt=
t+4tЃЌНтЕУЃКt=![]() ЃЎ
ЃЎ
ЃЈ2ЃЉ![]()
ЕуGдкABБпЩЯЪБЃЌЙ§ЕуGзїGHЁЭBCЃЌДЙзуЮЊHЃЌ
ЁпGHЁЮACЃЌ
ЫљвдЁїBGHЁзЁїBACЃЌ
Ёр![]() ЃЌМДЃК
ЃЌМДЃК 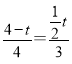 ЃЌ
ЃЌ
НтЕУЃКt=![]() ЃЎ
ЃЎ
ЃЈ3ЃЉЁпDFЁЮAC
ЁрЁїABCЁзЁїDBFЃЌ
Ёр![]() ЃЌ
ЃЌ
МД ЃЌНтЕУ
ЃЌНтЕУ![]()
ЂйЕБ![]() ЪБЃЌ
ЪБЃЌ
![]() =
= ![]()
ЂкЕБ![]() ЪБЃЌЩшFGНЛABгкЕуMЃЌЙ§ЕуMзїMHЁЭBCгкHЃЌЩшFH=MH=aЃЌ
ЪБЃЌЩшFGНЛABгкЕуMЃЌЙ§ЕуMзїMHЁЭBCгкHЃЌЩшFH=MH=aЃЌ
дђBH= ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУ![]()
![]()

ЁОЬтФПЁПФГаЃПЊеЙСЫЁАЮвЖСЪщЃЌЮвПьРжЁБЮЊжїЬтЕФЕїВщЛюЖЏЃЌЦфжаЦпФъМЖЖўАрШЋЬхЭЌбЇвЛИібЇЦкЦНОљвЛЬьдФЖСПЮЭтЪщМЎЫљгУЪБМфЕФЧщПіШчЯТБэЃК
ЪБМфЃЈаЁЪБЃЉ | 0.5 | 1 | 1.5 | 2 | 5 |
ШЫЪ§ЃЈУћЃЉ | 7ШЫ | 18ШЫ | 12ШЫ | 3ШЫ |
гЩгкЬюБэЕФЭЌбЇВЛаЁаФАбФЋЫЎЕЮдкСЫБэЩЯЃЌжТЪЙБэжаЪ§ОнВЛЭъећЃЌЕЋжЊЕРЫљгУЪБМфЮЊ1аЁЪБЕФШЫЪ§ЮЊШЋАрШЫЪ§ЕФ36%ЃЎНсКЯЩЯБэЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЦпФъМЖЖўАрЙВгаЖрЩйШЫЃП
ЃЈ2ЃЉбЇЩњЫљгУЪБМфЕФжкЪ§КЭжаЮЛЪ§ЗжБ№ЮЊЖрЩйаЁЪБЃП
ЃЈ3ЃЉШчЙћАбИУАрЕФбЇЩњЕФЫљгУЪБМфЧщПіЛцГЩЩШаЮЭГМЦЭМЃЌдђЫљгУЪБМфЮЊ2аЁЪБЕФШЫЪ§ЫљЖдгІЕФЩШаЮдВаФНЧЮЊЖрЩйЖШЃП