题目内容
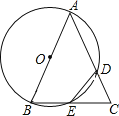
【题目】如图,在正方形ABCD中,AB=4,E是AB上一点,连接DE,过点A作AF⊥DE,垂足为F.⊙O经过点C、D、F,与AD相交于点G,且AB与⊙O相切,则AE的长为_____.
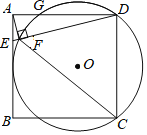
【答案】1
【解析】
设AB与⊙O相切于M,连接OM并反向延长交CD于N,则MN⊥AB,连接GF,根据垂径定理得到CN=DN,根据相似三角形的性质得到![]() =
=![]() ,如图,连接CG,根据相似三角形的性质得到
,如图,连接CG,根据相似三角形的性质得到![]() =
=![]() ,推出AG=EA,根据勾股定理列方程即可得到结论.
,推出AG=EA,根据勾股定理列方程即可得到结论.
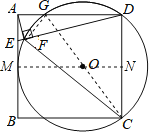
解:设AB与⊙O相切于M,连接OM并反向延长交CD于N,
则MN⊥AB,连接GF,
在正方形ABCD中,∵AB∥CD,
∴MN⊥CD,
∴CN=DN,
∵∠ADC=90°,
∴∠CDF+∠ADF=90°,
∵AF⊥DE,
∴∠AFD=90°,
∴∠DAF+∠ADF=90°,
∴∠DAF=∠CDF,
∵四边形GFCD是⊙O的内接四边形,
∴∠FCD+∠DGF=180°,
∵∠FGA+∠DGF=180°,
∴∠FGA=∠FCD,
∴△AFG∽△DFC,
∴![]() =
=![]() ,
,
如图,连接CG.
∵∠EAD=∠AFD=90°,∠EDA=∠ADF,
∴△EDA∽△ADF,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
在正方形ABCD中,DA=DC,
∴AG=EA,
∴DG=4﹣AE,
∵ON=![]() DG=2﹣
DG=2﹣![]() AE,
AE,
∴CG=2OM=2(4﹣ON)=4+AE,
∵DG2+CD2=CG2,
∴(4﹣AE)2+42=(4+AE)2,
∴AE=1.
故答案为:1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目