Question

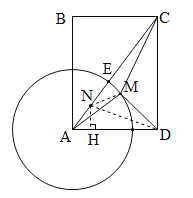
【题目】如图，已知矩形ABCD，AB=8，BC=6，以点A为圆心，5为半径作圆，点M为圆A上一动点，连接CM，DM,则CM+MD的最小值为_________．

Answer 1

【答案】

【解析】分析：连接AC交⊙A于点E，取AE的中点N，连接MN，ND，则CM+DM的最小值就是DN的长．作NH⊥AD，易求NH，AH，HD的长．在Rt△NHD中，由勾股定理即可得出结论．

详解：连接AC交⊙A于点E，取AE的中点N，连接MN，ND，则CM+DM的最小值就是DN的长．理由如下：

易知AC===10，AM=5，AN=2.5，

∴．

∵∠MAN=∠CAM（公共角），∴△MAN∽△CAM，∴，即MN=MC，

∴MC+DM=MN+DM≥DN，当N、M、D三点共线时等号成立．即CM+DM的最小值就是DN的长．

作NH⊥AD，易求NH=2.5×=2，AH=2.5×=1.5，HD=AD-AH=6-1.5=4.5，

∴ND===．

故答案为：．