题目内容
如图，点D、E分别为ABC边AC、AB上的一点，BD、CE交于点O，且BO=3DO，CO=3EO．求证：DE∥BC．
分析：依题意，BO=3DO，CO=3EO，则
=
．又其夹角为对顶角，所以△BOC与△DOE相似．根据相似三角形性质，运用平行线的判定得证．
| BO |
| DO |
| CO |
| EO |
解答：解：∵BO=3DO，CO=3EO，∴
=
．
∵∠BOC=∠DOE，
∴△BOC∽△DOE．
∴∠OBC=∠ODE．
∴DE∥BC．
| BO |
| DO |
| CO |
| EO |
∵∠BOC=∠DOE，
∴△BOC∽△DOE．
∴∠OBC=∠ODE．
∴DE∥BC．
点评：此题考查了相似三角形的判定和性质及平行线的判定，属基础题，比较简单．
练习册系列答案
名校课堂系列答案
相关题目
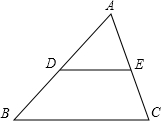如图，点D、E分别为△ABC的边AB、AC的中点，已知BC=6cm，则DE=
如图，点D，E分别为AB、AC上的两点且DE与BC不平行，请你添加任意一个条件，使△ABC与△ADE相似，添加的条件为
0）．点P、Q分别在抛物线y=
如图，点C、E分别为△ABD的边BD、AB上两点，且AE=AD，CE=CD，∠D=70゜，