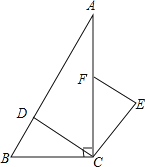
题目内容
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
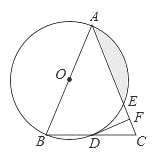
【答案】(1)见解析;(2)4π﹣8.
【解析】试题分析:(1)连接OD,易得∠ABC=∠ODB,由AB=AC,易得∠ABC=∠ACB,等量代换得∠ODB=∠ACB,利用平行线的判定得OD∥AC,由切线的性质得DF⊥OD,得出结论;
(2)连接OE,利用(1)的结论得∠ABC=∠ACB=67.5°,易得∠BAC=45°,得出∠AOE=90°,利用扇形的面积公式和三角形的面积公式得出结论.
试题解析:(1)连接OD,
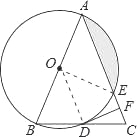
∵OB=OD,
∴∠ABC=∠ODB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ODB=∠ACB,
∴OD∥AC,
∵DF是⊙O的切线,
∴DF⊥OD,
∴DF⊥AC.
(2)连接OE,
∵DF⊥AC,∠CDF=22.5°,
∴∠ABC=∠ACB=67.5°,
∴∠BAC=45°,
∵OA=OE,
∴∠AOE=90°,
∵⊙O的半径为4,
∴S扇形AOE=4π,S△AOE="8" ,
∴S阴影=4π-8.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
【题目】学校李老师布置了两道解方程的作业题:
选用合适的方法解方程:
(1)x(x+1)=2x;(2)(x+1)(x﹣3)=7
以下是王萌同学的作业:
解:(1)移项,得x(x+1)﹣2x=0 分解因式得,x(x+1﹣2)=0 所以,x=0,或x﹣1=0 所以,x1=0,x2=1 | (2)变形得,(x+1)(x﹣3)=1×7 所以,x+1=7,x﹣3=1 解得,x1=6,x2=4 |
请你帮王萌检查他的作业是否正确,把不正确的改正过来.