Question

【题目】如图1，四边形ABCD的对角线AC，BD相交于点O，OB=OD，OC=OA+AB，AD=m，BC=n，∠ABD+∠ADB=∠ACB．

（1）填空：∠BAD与∠ACB的数量关系为；
（2）求 的值；
（3）将△ACD沿CD翻折，得到△A′CD（如图2），连接BA′，与CD相交于点P．若CD= ，求PC的长．

Answer 1

【答案】
（1）∠BAD+∠ACB=180°
（2）

解：如图1中，作DE∥AB交AC于E．

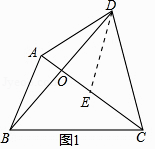
∴∠DEA=∠BAE，∠OBA=∠ODE，

∵OB=OD，

∴△OAB≌△OED，

∴AB=DE，OA=OE，设AB=DE=CE=CE=x，OA=OE=y，

∵∠EDA+∠DAB=180°，∠BAD+∠ACB=180°，

∴∠EDA=∠ACB，

∵∠DEA=∠CAB，

∴△EAD∽△ABC，

∴ = = = ，

∴ = ，

∴4y2+2xy﹣x2=0，

∴（ ）2+ ﹣1=0，

∴ = （负根已经舍弃），

∴ = ．

（3）

解：如图2中，作DE∥AB交AC于E．

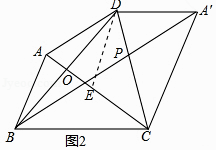
由（1）可知，DE=CE，∠DCA=∠DCA′，

∴∠EDC=∠ECD=∠DCA′，

∴DE∥CA′∥AB，

∴∠ABC+∠A′CB=180°，

∵△EAD∽△ACB，

∴∠DAE=∠ABC=∠DA′C，

∴∠DA′C+∠A′CB=180°，

∴A′D∥BC，

∴△PA′D∽△PBC，

∴ = = ，

∴ = ，即 =

∵CD= ，

∴PC=1．

【解析】解：（1.）如图1中，

在△ABD中，∵∠BAD+∠ABD+∠ADB=180°，
又∵∠ABD+∠ADB=∠ACB，
∴∠BAD+∠ACB=180°，
所以答案是∠BAD+∠ACB=180°．
【考点精析】根据题目的已知条件，利用相似三角形的判定与性质的相关知识可以得到问题的答案，需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．