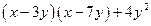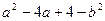题目内容
．已知多项式A=x2+2y2-z2，B=-4x2+3y2+2z2，且A+B+C=0，则C为（ ）
| A．5x2-y2-z2 | B．3x2-5y2-z2 | C．3x2-y2-3z2 | D．3x2-5y2+z2 |
B
由于A+B+C=0，则C=-A-B，代入A和B的多项式即可求得C．
解：由于多项式A=x2+2y2-z2，B=-4x2+3y2+2z2且A+B+C=0，
则C=-A-B=-（x2+2y2-z2）-（-4x2+3y2+2z2）=-x2-2y2+z2+4x2-3y2-2z2=3x2-5y2-z2．
故答案选B。
解：由于多项式A=x2+2y2-z2，B=-4x2+3y2+2z2且A+B+C=0，
则C=-A-B=-（x2+2y2-z2）-（-4x2+3y2+2z2）=-x2-2y2+z2+4x2-3y2-2z2=3x2-5y2-z2．
故答案选B。
练习册系列答案
相关题目
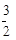x2+6x+2中，-x2和 是同类项，8x和 是同类项，2和 是同类项.
____________________．
=▼.
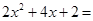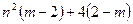(2)
