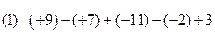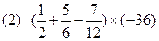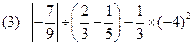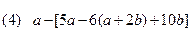题目内容
．观察下列各式：(x－1)(x＋1)＝x2―1；(x―1)(x2＋x＋1)＝x3―1；(x―1)(x3＋x2＋x＋1)
＝x4－1……；根据前面各式的规律可得到(x－1)(xn＋xn－1＋xn－2＋…＋x＋1)＝______．
＝x4－1……；根据前面各式的规律可得到(x－1)(xn＋xn－1＋xn－2＋…＋x＋1)＝______．
xn＋1－1
分析：观察其右边的结果：第一个是x2-1；第二个是x3-1；…依此类推，则第n个的结果即可求得．
解：（x-1）（xn+xn-1+…x+1）=xn+1-1．
练习册系列答案
高效智能课时作业系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
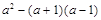的结果为（ ）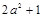
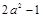
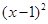相等的是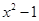 
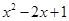
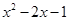
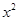
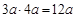
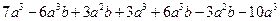的值．题目出完后，小聪说：“老师给的条件a=0.35，b= -0.28是多余的．”小明说：“不给这两个条件，就不能求出结果，所以不是多余的．”你认为他们谁说的有道理？为什么？
。
＝ .
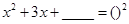