题目内容
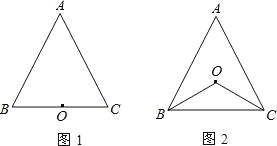
【题目】将一副直角三角尺(即直角三角形AOB和直角三角形COD)的直角顶点O的重合,其中,在△AOB中,∠A=60°,∠B=30°,∠AOB=90°;在△COD中,∠C=∠D=45°,∠COD=90°.
(1)如图1,当OA在∠COD的外部,且∠AOC=45°时,①试说明CO平分∠AOB; ②试说明OA∥CD(要求书写过程);
(2)如图2,绕点O旋转直角三角尺AOB,使OA在∠COD的内部,且CD∥OB,试探索∠AOC=45°是否成立,并说明理由.

【答案】(1)①证明见解析,②证明见解析;(2)成立,理由见解析
【解析】
(1)①当∠AOC=45°时,根据条件可求得∠COB=45°可说明CO平分∠AOB;②设CD、OB交于点E,则可知OE=CE,可证得OB⊥CD,结合条件可证明OA∥CD;
(2)由平行可得到∠D=∠BOD=45°,则可得到∠AOD=45°,可得到结论.
解: 解:(1)①∵∠AOB=90°,∠AOC=45°,
∴∠COB=90°﹣45°=45°,
∴∠AOC=∠COB,
即OC平分∠AOB;
②如图,设CD、OB交于点E,
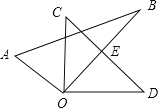
∵∠C=45°,
∴∠C=∠COB,
∴∠CEO=90°,
∵∠AOB=90°,
∴∠AOB+∠OEC=180°,
∴AO∥CD;
(2)∠AOC=45°,理由如下:
∵CD∥OB,
∴∠DOB=∠D=45°,
∴∠AOD=90°﹣∠DOB=45°,
∴∠AOC=90°﹣∠AOD=45°.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目