题目内容
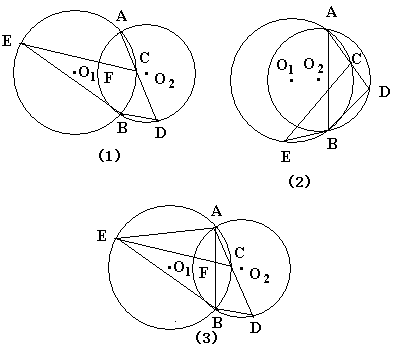
如图，已知：⊙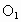
与⊙
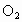相交于A，B两点，经过A点的直线分别交⊙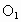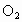，⊙于C，D两点(C，D不与B重合)，连结BD，过D作BD的平行线交⊙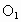于点E，连结BE．
(1)求证：BE是⊙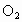的切线．(图(1))
(2)如图(2)，若两圆圆心在公共弦AB的同侧，其他条件不变，判断BE和⊙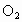的位置关系．(不要求证明)
(3)若点C为劣弧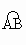
的中点，其他条件不变，连结AB，AE，AB与CE交于点F，如图(3)，写出图中所有的相似三角形．(不另外连线，不要求证明)
答案：略
解析：
解析：
|
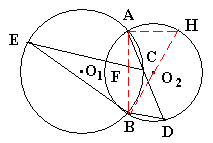
解： (1)过B作⊙ 的直径BH，连结AB，AH，
则∠ABH＋∠H=90°，∠H=∠ADB，∠ACE=∠ABE，∠ABE=∠ADB， ∴∠ABH＋∠ABE=90°，即BE⊥BH， ∴BE与⊙ (2)BE仍是⊙ (3)△AFC∽△ABD∽△EFB∽△EAC． |
练习册系列答案
相关题目
O相交于点P，AB与⊙O相切于点B，BP的延长线交直线l于点C．
如图，已知直线l与⊙O相离，OA⊥l于点A，OA=5，0A与⊙0相交于点P，AB与⊙O相切于点B，BP的延长线交直线l于点C
，求⊙O的半径和线段PB的长；
，求⊙O的半径和线段PB的长；