题目内容
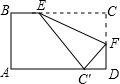 如图,把矩形纸片折叠,使点C落在AD边的中点C′处,设折痕为EF,AB=3,BC=4,则CE:BE=________.
如图,把矩形纸片折叠,使点C落在AD边的中点C′处,设折痕为EF,AB=3,BC=4,则CE:BE=________.
13:3
分析:过E作EG⊥AD于G,根据图形翻折不变性可知△CEF≌△C'EF,设BE=x,则CE=C′E=4-x,在Rt△BGC′中,利用勾股定理即可求出x的值,由CE=BC-BE即可求解.
解答: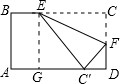 解:过E作EG⊥AD于G,
解:过E作EG⊥AD于G,
∵△CGE是△EFC沿EF折叠而成,
∴CE=C′E,
∵C′是AD的中点,
∴AC′= AD=
AD= ×4=2,
×4=2,
∵AB⊥AD,EG⊥AD,BE∥AD,∠B=90°,
∴四边形ABEG是矩形,
∴AG=BE,
设BE=x,则BC=C′E=4-x,C′G=2-AG=2-x,
在Rt△C′EG中,C′E2=EG2+C′G2,即(4-x)2=32+(2-x)2,
解得x= ,
,
故CE=4- =
= ,
,
∴ =
=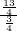 =
= .
.
故答案为:13:3.
点评:本题考查的是图形折叠的性质及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
分析:过E作EG⊥AD于G,根据图形翻折不变性可知△CEF≌△C'EF,设BE=x,则CE=C′E=4-x,在Rt△BGC′中,利用勾股定理即可求出x的值,由CE=BC-BE即可求解.
解答:
 解:过E作EG⊥AD于G,
解:过E作EG⊥AD于G,∵△CGE是△EFC沿EF折叠而成,
∴CE=C′E,
∵C′是AD的中点,
∴AC′=
 AD=
AD= ×4=2,
×4=2,∵AB⊥AD,EG⊥AD,BE∥AD,∠B=90°,
∴四边形ABEG是矩形,
∴AG=BE,
设BE=x,则BC=C′E=4-x,C′G=2-AG=2-x,
在Rt△C′EG中,C′E2=EG2+C′G2,即(4-x)2=32+(2-x)2,
解得x=
 ,
,故CE=4-
 =
= ,
,∴
 =
=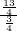 =
= .
.故答案为:13:3.
点评:本题考查的是图形折叠的性质及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
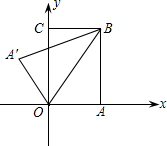 如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB将纸片沿OB折叠,使A落在A′的位置,若OB=
如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB将纸片沿OB折叠,使A落在A′的位置,若OB=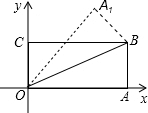 如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB,将纸片OABC沿OB折叠,使点A落在A1的位置.若OB=
如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB,将纸片OABC沿OB折叠,使点A落在A1的位置.若OB= 如图,把矩形纸片ABCD沿折叠,使点B落在边AD上的点B′处,点A落在点A′处;
如图,把矩形纸片ABCD沿折叠,使点B落在边AD上的点B′处,点A落在点A′处;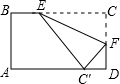 如图,把矩形纸片折叠,使点C落在AD边的中点C′处,设折痕为EF,AB=3,BC=4,则CE:BE=
如图,把矩形纸片折叠,使点C落在AD边的中点C′处,设折痕为EF,AB=3,BC=4,则CE:BE=