��Ŀ����
����Ŀ���Ķ����⣬���ǰ�������������һ���ı��θ����е�õ����ı��ν��е��ı��Σ���ͼ1�����ı���ABCD�У�E��F��G��H�ֱ��DZ�AB��BC��CD��DA���е㣬�������Ӹ����е�õ��е��ı���EFGH�� 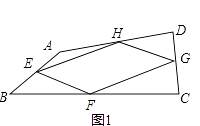
��1������е��ı���EFGH����״����
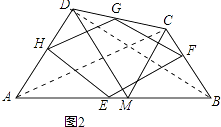
��2����ͼ2�����ı���ABCD�У���M��AB���ҡ�AMD�͡�MCBΪ�ȱ������Σ�E��F��G��H�ֱ�ΪAB��BC��CD��AD���е㣬���ж��ı���EFGH����״��֤���� 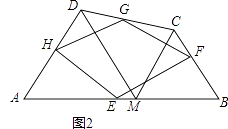
���𰸡�
��1��ƽ���ı���
��2���⣺�ı���EFGHΪ���Σ��������£�
����AC��BD����ͼ2��ʾ��
�ߡ�AMD�͡�MCBΪ�ȱ������Σ�
��AM=DM����AMD=��CMB=60�㣬CM=BM��
���AMC=��DMB��
�ڡ�AMC�͡�DMB�У�
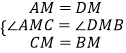 ��
��
���AMC�ա�DMB��SAS����
��AC=DB��
�ߡ�E��F��G��H�ֱ��DZ�AB��BC��CD��DA���е㣬
��EF�ǡ�ABC����λ�ߣ�GH�ǡ�ACD����λ�ߣ�HE�ǡ�ABD����λ�ߣ�
��EF��AC��EF= ![]() AC��GH��AC��GH=
AC��GH��AC��GH= ![]() AC��HE=
AC��HE= ![]() DB��
DB��
��EF��GH��EF=GH��
���ı���EFGH��ƽ���ı��Σ�
��AC=DB��
��EF=HE��
���ı���EFGHΪ���Σ�
���������⣺��1���е��ı���EFGH��ƽ���ı��Σ� �������£�����AC����ͼ1��ʾ��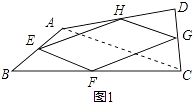
��E��F��G��H�ֱ��DZ�AB��BC��CD��DA���е㣬
��EF�ǡ�ABC����λ�ߣ�GH�ǡ�ACD����λ�ߣ�
��EF��AC��EF= ![]() AC��GH��AC��GH=
AC��GH��AC��GH= ![]() AC��
AC��
��EF��GH��EF=GH��
���ı���EFGH��ƽ���ı��Σ�
���Դ��ǣ�ƽ���ı��Σ�

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ���»����������¹������������30�������ۺ��ۼ������ȫ�������������510Ԫ��
���� | ���� | |
���ۣ�Ԫ/���� | 95 | 80 |
�ۼۣ�Ԫ/���� | 110 | 100 |
��1�������������������ٸ���
��2������8����������������ۼ��������������ȣ�