��Ŀ����
����Ŀ����ͼ����֪�߶�AB�Ĵ�ֱƽ����CP��AB�ڵ�P����AP=2PC���������߶�AB����������D��E��ʹ������AD=DC=CE=EB���������¼ס�������������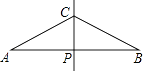
�ף��ֱ�����ACP����BCP��ƽ���ߣ��ֱ�AB��D��E����D��E��Ϊ����
�ң��ֱ���AC��BC�Ĵ�ֱƽ���ߣ��ֱ�AB��D��E����D��E���㼴Ϊ����
����˵����ȷ���ǣ� ��
A.�ס��Ҷ���ȷ
B.�ס��Ҷ�����
C.����ȷ���Ҵ���
D.�״�������ȷ
���𰸡�D
���������ף���ȻCP= AP������A�١�ACP��
����A�١�ACD���ײ���ȷ��
�ҡ�CP���߶�AB���д��ߣ�
���ABC�ǵ��������Σ���AC=BC����A=��B��
��AC��BC֮�д��߷ֱ�AB��D��E��
���A=��ACD����B=��BCE��
�ߡ�A=��B��
���A=��ACD����B=��BCE��
��AC=BC��
���ACD�ա�BCE��
��AD=EB��
��AD=DC��EB=CE��
��AD=DC=EB=CE������ȷ��
�ʴ�Ϊ��D
�������߶ε������˵�ľ�����ȵĵ㣬���߶εĴ�ֱƽ�����ϣ����߶δ�ֱƽ�����ϵĵ����߶ε������˵�ľ�����ȣ��߶�AB�Ĵ�ֱƽ����CP�õ�AC=BC���õ�����.

��ϰ��ϵ�д�
�����Ŀ



