题目内容
【题目】.已知，如图：在平面直角坐标系中，O为坐标原点，四边形OABC是长方形，点A、C、D的坐标分别为A（9，0）、C（0，4），D（5，0），点P从点O出发，以每秒1个单位长度的速度沿O 
C B A运动，点P的运动时间为t秒.
（1）当t=2时，求直线PD的解析式。
（2）当P在BC上，OP+PD有最小值时，求点P的坐标。
（3）当t为何值时，△ODP是腰长为5的等腰三角形？（直接写出t的值）.
【答案】（1）y=-
x+2；（2）P(2.5，4) ；（3）6或7或12或14；
【解析】
（1）先求得点P的坐标，再利用待定系数法求直线PD的解析式即可；（2）先确定点P的位置，再求点P的坐标即可；（3）分OD=DP=5、OD=OP=5、PO=PD=5三种情况求点t得值即可.
(1)当t=2时，OP=2×1=2，又C(0，4)，所以P(0，2).
设直线PD的函数解析式为y=kx+b，
把x=0，y=2，x=5，y=0分别代入上式，得
，
解得，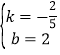
∴当t=2时，直线PD的函数解析式为y=-x+2.
(2)如图，过点D作DF⊥CB，垂足为F，延长DF到E，使FE=FD，连接OE交CB于点P.
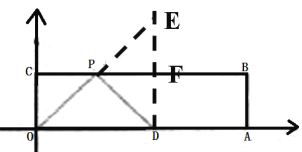
由作法可知PF是线段DE的垂直平分线，所以PD=PE.
所以OP+PD=OP+PE=OE.
根据两点之间，线段最短，此时OP+PD的值最小.
易证PF是的中位线，所以PF=
∴CP=CF-PF=OD-PF=5-
=,
∴点P的坐标为(，4).
(3)当t=6，t=7，或t=12，或t=14时，是腰长为5的等腰三角形.（如图点P的四个位置时满足条件 ）.
练习册系列答案
相关题目
