题目内容
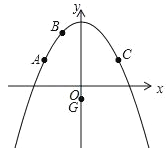
【题目】二次函数y=ax2+c的图象经过点A(﹣4,3),B(﹣2,6),点A关于抛物线对称轴的对称点为点C,点P是抛物线对称轴右侧图象上的一点,点G(0,﹣1).
(1)求出点C坐标及抛物线的解析式;
(2)若以A,C,P,G为顶点的四边形面积等于30时,求点P的坐标;
(3)若Q为线段AC上一动点,过点Q平行于y轴的直线与过点G平行于x轴的直线交于点M,将△QGM沿QG翻折得到△QGN,当点N在坐标轴上时,求Q点的坐标.
【答案】(1)y=﹣![]() x2+7,点C的坐标为(4,3);(2)P点坐标为(
x2+7,点C的坐标为(4,3);(2)P点坐标为(![]() ,
,![]() )或(6,﹣2);(3)Q点坐标为(﹣4,3)或(﹣4,﹣3)或(﹣
)或(6,﹣2);(3)Q点坐标为(﹣4,3)或(﹣4,﹣3)或(﹣![]() ,3)或(
,3)或(![]() ,3).
,3).
【解析】(1)利用待定系数法求抛物线解析式,然后利用抛物线的对称性确定C点坐标;
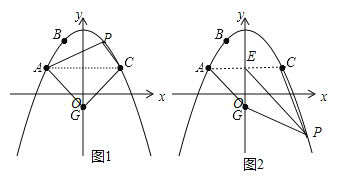
(2)设P(x,﹣![]() x2+7)(x>0),讨论:当点P在AC上方时,如图1,利用S四边形AGCP=S△GAC+S△PAC列方程
x2+7)(x>0),讨论:当点P在AC上方时,如图1,利用S四边形AGCP=S△GAC+S△PAC列方程![]() 84+
84+![]() 8(﹣
8(﹣![]() x2+7﹣3)=30,当点P在AC下方时,如图2,AC与y轴交于点E,利用S四边形AGPC=S△GAE+S△PEG+S△PEC列方程
x2+7﹣3)=30,当点P在AC下方时,如图2,AC与y轴交于点E,利用S四边形AGPC=S△GAE+S△PEG+S△PEC列方程![]() 44+
44+![]() x4+
x4+![]() 4(3+
4(3+![]() x2﹣7)=30,然后分别解方程可得到对应的P点坐标;
x2﹣7)=30,然后分别解方程可得到对应的P点坐标;
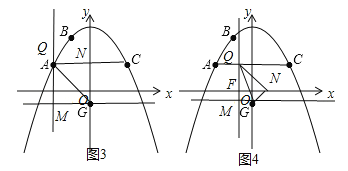
(3)当点N落在y轴上,如图3,利用折叠性质得∠QNG=∠QMG=90°,QN=QM=4,易得Q点的坐标;当点N落在x轴上,QM与x轴交于点F,如图4,设Q(t,3)(﹣4≤t<0),利用折叠性质得∠QNG=∠QMG=90°,QN=QM=4,GN=GM=﹣t,由于FN=![]() ,OF=﹣t,ON=
,OF=﹣t,ON=![]() ,则
,则![]() ﹣t=
﹣t=![]() ,解方程得到此时Q点的坐标,当0<t≤4,同理可得Q点的坐标.
,解方程得到此时Q点的坐标,当0<t≤4,同理可得Q点的坐标.
(1)∵二次函数y=ax2+c的图象经过点A(﹣4,3),B(﹣2,6),∴![]() ,解得:
,解得: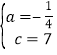 ,∴抛物线的解析式为y=﹣
,∴抛物线的解析式为y=﹣![]() x2+7.
x2+7.
∵二次函数y=ax2+c的图象的对称轴为y轴,点A(﹣4,3),∴点C的坐标为(4,3).
(2)设P(x,﹣![]() x2+7)(x>0),当点P在AC上方时,如图1,S四边形AGCP=S△GAC+S△PAC=
x2+7)(x>0),当点P在AC上方时,如图1,S四边形AGCP=S△GAC+S△PAC=![]() 84+
84+![]() 8(﹣
8(﹣![]() x2+7﹣3),∴
x2+7﹣3),∴![]() 84+
84+![]() 8(﹣
8(﹣![]() x2+7﹣3)=30,解得:x1=
x2+7﹣3)=30,解得:x1=![]() ,x2=﹣
,x2=﹣![]() (舍去),此时P点坐标为(
(舍去),此时P点坐标为(![]() );
);
当点P在AC下方时,如图2,AC与y轴交于点E,S四边形AGPC=S△GAE+S△PEG+S△PEC=![]() 44+
44+![]() x4+
x4+![]() 4(3+
4(3+![]() x2﹣7),∴
x2﹣7),∴![]() 44+
44+![]() x4+
x4+![]() 4(3+
4(3+![]() x2﹣7)=30,解得:x1=6,x2=﹣10(舍去),此时P点坐标为(6,﹣2).
x2﹣7)=30,解得:x1=6,x2=﹣10(舍去),此时P点坐标为(6,﹣2).
综上所述:P点坐标为(![]() )或(6,﹣2);
)或(6,﹣2);
(3)QN=3﹣(﹣1)=4,当点N落在y轴上,如图3.
∵△QGM沿QG翻折得到△QGN,∴∠QNG=∠QMG=90°,QN=QM=4,∴N点为AC与y轴的交点,∴Q点的坐标为(﹣4,3)或(﹣4,﹣3);
当点N落在x轴上,QM与x轴交于点F,如图4,设Q(t,3)(﹣4≤t<0)
∵△QGM沿QG翻折得到△QGN,∴∠QNG=∠QMG=90°,QN=QM=4,GN=GM=﹣t.在Rt△OFN中,FN=![]() =
=![]() ,而OF=﹣t,ON=
,而OF=﹣t,ON=![]() ﹣t=
﹣t=![]() ,解得:t=﹣
,解得:t=﹣![]() ,此时Q点的坐标为(﹣
,此时Q点的坐标为(﹣![]() ,3),当0<t≤4,易得Q点的坐标为(
,3),当0<t≤4,易得Q点的坐标为(![]() ,3).
,3).
综上所述:Q点坐标为(﹣4,3)或(﹣4,﹣3)或(﹣![]() ,3)或(
,3)或(![]() ,3).
,3).