题目内容
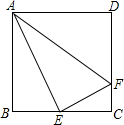如图：在正方形ABCD中，E为BC中点，点F在CD边上，且DF=3FC，连接AE、AF、EF，（1）求证△ECF∽△ABE；
（2）图中是否存在与∠EAF相等的角？若存在，请写出并加以证明；若不存在，请说明理由．
分析：（1）根据正方形的性质得出AB=BC=CD，∠B=∠C=90°，再根据已知条件得出
=
=
，能证明△ECF∽△ABE；
（2）先判断图中与∠EAF相等的角，再进行证明，根据△ECF∽△ABE，则∠FEC=∠BAE，且
=
=
，再证明△AEF∽△ABE，则∠EAF=∠BAE，∠FEC=∠EAF．
| FC |
| EC |
| BE |
| AB |
| 1 |
| 2 |
（2）先判断图中与∠EAF相等的角，再进行证明，根据△ECF∽△ABE，则∠FEC=∠BAE，且
| EF |
| AE |
| EC |
| AB |
| BE |
| AB |
解答：证明：（1）由正方形ABCD得AB=BC=CD，∠B=∠C=90°（2分）
∵E为BC中点，DF=3FC，
∴BE=EC=
AB，FC=
CD=
AB，
∴
=
=
（2分）
在△ECF和△ABE中，
∵
=
且∠B=∠C
∴△ECF∽△ABE（1分）．
（2）图中存在与∠EAF相等的角，分别是∠BAE和∠FEC（2分）．
∵△ECF∽△ABE，∴∠FEC=∠BAE，且
=
=
（2分）．
在△ABE中，∵∠B=90°，∴∠BEA+∠BAE=90°∴∠FEC+∠BEA=90°，
∴∠AEF=90°，∠AEF=∠B（1分）
又∵
=
，∴△AEF∽△ABE，
∴∠EAF=∠BAE同理∠FEC=∠EAF（2分）．
∵E为BC中点，DF=3FC，
∴BE=EC=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∴
| FC |
| EC |
| BE |
| AB |
| 1 |
| 2 |
在△ECF和△ABE中，
∵
| FC |
| EC |
| BE |
| AB |
∴△ECF∽△ABE（1分）．
（2）图中存在与∠EAF相等的角，分别是∠BAE和∠FEC（2分）．
∵△ECF∽△ABE，∴∠FEC=∠BAE，且
| EF |
| AE |
| EC |
| AB |
| BE |
| AB |
在△ABE中，∵∠B=90°，∴∠BEA+∠BAE=90°∴∠FEC+∠BEA=90°，
∴∠AEF=90°，∠AEF=∠B（1分）
又∵
| EF |
| AE |
| BE |
| AB |
∴∠EAF=∠BAE同理∠FEC=∠EAF（2分）．
点评：本题考查了相似三角形的判定和性质以及正方形的性质，是综合题难度偏大．
练习册系列答案
相关题目
如图：在正方形网格上有△ABC，△DEF，说明这两个三角形相似，并求出它们的相似比．
，交BC于点E．
23、如图，在Rt△ABC中，∠BAC=90°，AD=CD，点E是边AC的中点，连接DE，DE的延长线与边BC相交于点F，AG∥BC，交DE于点G，连接AF、CG．
如图，在Rt△ABC中，∠C=90°，以斜边AB为边向外作正方形ABDE，且正方形对角线交于点O，连接OC，已知AC=5，OC=6