题目内容
【题目】在平面直角坐标系中,如图1,将n个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在x轴和y轴的正半轴上,设抛物线y=ax2+bx+c(a<0)过矩形顶点B、C. 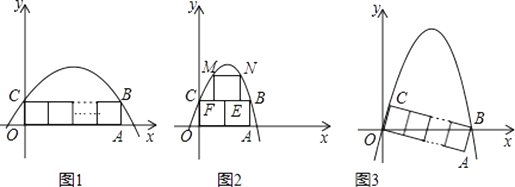
(1)当n=1时,如果a=﹣1,试求b的值;
(2)当n=2时,如图2,在矩形OABC上方作一边长为1的正方形EFMN,使EF在线段CB上,如果M,N两点也在抛物线上,求出此时抛物线的解析式;
(3)将矩形OABC绕点O顺时针旋转,使得点B落到x轴的正半轴上,如果该抛物线同时经过原点O. ①试求当n=3时a的值;
②直接写出a关于n的关系式.
【答案】
(1)解:∵抛物线过矩形顶点B、C,其中C(0,1),B(n,1)
∴当n=1时,抛物线对称轴为直线x= ![]() ,
,
∴ ![]() ,
,
∵a=﹣1,
∴b=1,
答:b的值是1
(2)解:设所求抛物线解析式为y=ax2+bx+1,
由对称性可知抛物线经过点B(2,1)和点M( ![]() ,2),
,2),
则 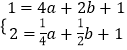 ,
,
解得 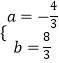
∴所求抛物线解析式为 ![]() ,
,
答:此时抛物线的解析式是 ![]()
(3)解:①当n=3时,OC=1,BC=3,
设所求抛物线解析式为y=ax2+bx,
过C作CD⊥OB于点D,
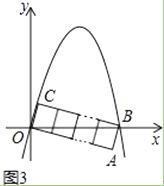
则Rt△OCD∽Rt△OBC,
∴ ![]() ,
,
设OD=t,则CD=3t,
∵OD2+CD2=OC2,
∴(3t)2+t2=12,
∴ ![]() ,
,
∴C( ![]() ,
, ![]() ),
),
又∵B( ![]() ,0),
,0),
∴把B、C坐标代入抛物线解析式,得 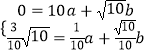 ,
,
解得:a=﹣ ![]() ,
,
a关于n的关系式是 ![]()
【解析】(1)根据已知得到抛物线对称轴为直线x= ![]() ,代入即可求出b;(2)设所求抛物线解析式为y=ax2+bx+1,由对称性可知抛物线经过点B(2,1)和点M(
,代入即可求出b;(2)设所求抛物线解析式为y=ax2+bx+1,由对称性可知抛物线经过点B(2,1)和点M( ![]() ,2),把B、M的坐标代入得到方程组
,2),把B、M的坐标代入得到方程组 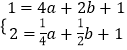 ,求出a、b的值即可得到抛物线解析式;(3)①当n=3时,OC=1,BC=3,设所求抛物线解析式为y=ax2+bx,过C作CD⊥OB于点D,则Rt△OCD∽Rt△OBC,得出
,求出a、b的值即可得到抛物线解析式;(3)①当n=3时,OC=1,BC=3,设所求抛物线解析式为y=ax2+bx,过C作CD⊥OB于点D,则Rt△OCD∽Rt△OBC,得出 ![]() ,设OD=t,则CD=3t,根据勾股定理OD2+CD2=OC2 , 求出t,得出C的坐标,把B、C坐标代入抛物线解析式即可得到方程组,求出a即可;②根据(1)、(2)①总结得到答案.
,设OD=t,则CD=3t,根据勾股定理OD2+CD2=OC2 , 求出t,得出C的坐标,把B、C坐标代入抛物线解析式即可得到方程组,求出a即可;②根据(1)、(2)①总结得到答案.
【考点精析】根据题目的已知条件,利用解二元一次方程组和勾股定理的概念的相关知识可以得到问题的答案,需要掌握二元一次方程组:①代入消元法;②加减消元法;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

 应用题作业本系列答案
应用题作业本系列答案