题目内容
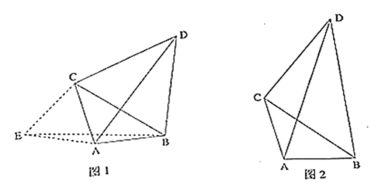
【题目】如图,在等边![]() 中,
中,![]() 分别为
分别为![]() 的中点,延长
的中点,延长![]() 至点
至点![]() ,使
,使![]() ,连结
,连结![]() 和
和![]() .
.
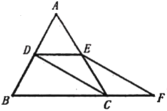
(1)求证:![]()
(2)猜想:![]() 的面积与四边形
的面积与四边形![]() 的面积的关系,并说明理由.
的面积的关系,并说明理由.
【答案】(1)见解析;(2)相等,理由见解析.
【解析】
(1)直接利用三角形中位线定理得出DE∥BC,且DE=![]() BC,再利用平行四边形的判定方法得出答案;
BC,再利用平行四边形的判定方法得出答案;
(2)分别过点A,D,作AM⊥DE,DN⊥BC,根据等底等高的三角形面积相等求得S△ADE=S△ECF,再根据S△ADE +S四边形BDEC=S△ECF +S四边形BDEC可得出结果.
(1)证明:∵D,E分别为AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,DE=![]() BC.
BC.
∵CF=![]() BC,
BC,
∴DE∥CF,DE=CF,
∴四边形DEFC为平行四边形,
∴CD=EF;
(2)解:相等.理由如下:
分别过点A,D,作AM⊥DE,DN⊥BC,则∠AMD=∠DNB=90°,
∵DE∥BC,
∴∠ADM=∠DBN.
∵AD=DB,
∴△ADM≌△DBN(AAS),
∴AM=DN.
又∵DE=CF,
∴S△ADE=S△ECF (等底等高的三角形面积相等).
∴S△ADE +S四边形BDEC=S△ECF +S四边形BDEC,
∴△ABC的面积等于四边形BDEF的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目