Question

【题目】问题背景：如图，点为线段外一动点，且，若，，连接，求的最大值．解决方法：以为边作等边，连接，推出，当点在的延长线上时，线段取得最大值．

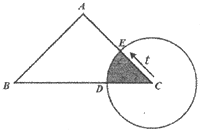
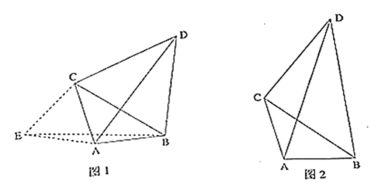
问题解决：如图，点为线段外一动点，且，若，，连接，当取得最大值时，的度数为_________．

Answer 1

【答案】

【解析】

以AC为直角边，作等腰直角三角形CEA，CE =CA，∠ECA=90°，连接EB，利用SAS证出△ECB≌△ACD，从而得出EB=AD，然后根据两点之间线段最短即可得出当AD取得最大值时，E、A、B三点共线，然后求出∠CAB的度数，根据等边对等角和三角形的内角和定理即可求出∠ACB，从而求出∠ACD．

解：以AC为直角边，作等腰直角三角形CEA，CE =CA，∠ECA=90°，连接EB

∵

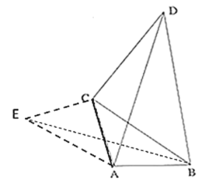
∴∠ECA＋∠ACB=∠BCD＋∠ACB

∴∠ECB=∠ACD

在△ECB和△ACD中

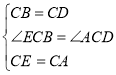
∴△ECB≌△ACD

∴EB=AD

∴当AD取得最大值时，EB也取得最大值

根据两点之间线段最短可知EB≤EA＋EB，当且仅当E、A、B三点共线时取等号

即当AD取得最大值时，E、A、B三点共线，

∵△CEA为等腰直角三角形

∴∠CAE=45°

∴此时∠CAB=180°―CAE=135°

∵

∴∠ACB=∠ABC=（180°－∠CAB）=°

∴∠ACD=∠ACB＋∠BCD=

故答案为：．