题目内容
已知:如图,在梯形ABCD中,∠BCD=90°,tan∠ADC=2,点E在梯形内,点F在梯形外,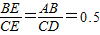 ,∠EDC=∠FBC,且DE=BF.
,∠EDC=∠FBC,且DE=BF.(1)判断△ECF的形状特点,并证明你的结论;
(2)若∠BEC=135°,求∠BFE的正弦值.
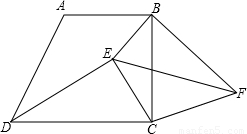
【答案】分析:(1)是等腰直角三角形,理由是作AH⊥CD于H,根据梯形ABCD得出AB∥CD,AH=BC,AB=CH,推出DH=CH,CD=2DH,由tan∠ADC=2,推出AH=2DH=CD=BC,根据SAS证出△EDC≌△FBC,推出CE=CF,∠ECD=∠FCB,证出∠ECF=∠BCD=90°即可得到答案;
(2)可求出∠CEF=45°,CE=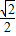 EF,由已知,求出∠BEF=90°,
EF,由已知,求出∠BEF=90°, =
=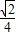 ,设BE=
,设BE=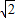 ,EF=4,根据勾股定理求出BF=
,EF=4,根据勾股定理求出BF=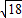 ,根据锐角三角函数的定义即可求出答案.
,根据锐角三角函数的定义即可求出答案.
解答:(1)答:是等腰直角三角形,
证明:作AH⊥CD于H,
∵梯形ABCD中,∠BCD=90°,tan∠ADC=2,即∠ADC≠90°,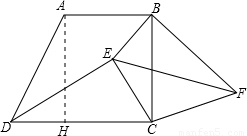
∴AB∥CD,
∴四边形AHCB是平行四边形,
∴AH=BC,AB=CH,
又∵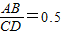 ,即CH+DH=2AB=2CH,
,即CH+DH=2AB=2CH,
∴DH=CH,CD=2DH,
∵tan∠ADC=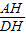 =2,
=2,
∴AH=2DH=CD=BC,
在△EDC和△FBC中,
又∵∠EDC=∠FBC,DE=BF,
∴△EDC≌△FBC
∴CE=CF,∠ECD=∠FCB.
∵∠ECD+∠ECB=∠BCD=90°,
∴∠FCB+∠ECB=90°,
即∠ECF=90°.
∴△ECF是等腰直角三角形.
(2)解:∵在等腰Rt△ECF中,∠ECF=90°,
∴∠CEF=45°,CE=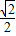 EF,
EF,
又∵∠BEC=135°,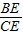 =0.5,
=0.5,
∴∠BEF=90°,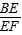 =
=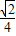 ,
,
不妨设BE=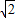 ,EF=4,则由勾股定理得:BF=
,EF=4,则由勾股定理得:BF=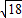 ,
,
∴sin∠BFE=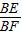 =
=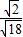 =
= ,
,
答:∠BFE的正弦值是 .
.
点评:本题主要考查对直角梯形,全等三角形的性质和判定,勾股定理,等腰三角形的性质和判定,锐角三角函数的定义,平行四边形的性质和判定等知识点的理解和掌握,此题是一个拔高的题目,有一定的难度.
(2)可求出∠CEF=45°,CE=
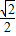 EF,由已知,求出∠BEF=90°,
EF,由已知,求出∠BEF=90°, =
=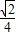 ,设BE=
,设BE=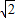 ,EF=4,根据勾股定理求出BF=
,EF=4,根据勾股定理求出BF=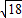 ,根据锐角三角函数的定义即可求出答案.
,根据锐角三角函数的定义即可求出答案.解答:(1)答:是等腰直角三角形,
证明:作AH⊥CD于H,
∵梯形ABCD中,∠BCD=90°,tan∠ADC=2,即∠ADC≠90°,

∴AB∥CD,
∴四边形AHCB是平行四边形,
∴AH=BC,AB=CH,
又∵
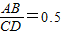 ,即CH+DH=2AB=2CH,
,即CH+DH=2AB=2CH,∴DH=CH,CD=2DH,
∵tan∠ADC=
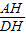 =2,
=2,∴AH=2DH=CD=BC,
在△EDC和△FBC中,
又∵∠EDC=∠FBC,DE=BF,
∴△EDC≌△FBC
∴CE=CF,∠ECD=∠FCB.
∵∠ECD+∠ECB=∠BCD=90°,
∴∠FCB+∠ECB=90°,
即∠ECF=90°.
∴△ECF是等腰直角三角形.
(2)解:∵在等腰Rt△ECF中,∠ECF=90°,
∴∠CEF=45°,CE=
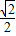 EF,
EF,又∵∠BEC=135°,
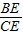 =0.5,
=0.5,∴∠BEF=90°,
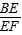 =
=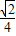 ,
,不妨设BE=
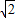 ,EF=4,则由勾股定理得:BF=
,EF=4,则由勾股定理得:BF=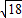 ,
,∴sin∠BFE=
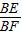 =
=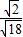 =
= ,
,答:∠BFE的正弦值是
 .
.点评:本题主要考查对直角梯形,全等三角形的性质和判定,勾股定理,等腰三角形的性质和判定,锐角三角函数的定义,平行四边形的性质和判定等知识点的理解和掌握,此题是一个拔高的题目,有一定的难度.

练习册系列答案
相关题目
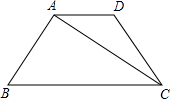 已知:如图,在梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,求AC的长及梯形面积S.
已知:如图,在梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,求AC的长及梯形面积S.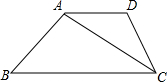 已知:如图,在梯形ABCD中,AD∥BC,∠B=45°,∠BAC=105°,AD=CD=4,
已知:如图,在梯形ABCD中,AD∥BC,∠B=45°,∠BAC=105°,AD=CD=4,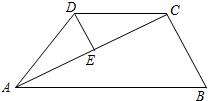 已知:如图,在梯形ABCD中,AB∥CD,AC⊥BC,AC平分∠DAB,点E为AC的中点.求证:DE=
已知:如图,在梯形ABCD中,AB∥CD,AC⊥BC,AC平分∠DAB,点E为AC的中点.求证:DE=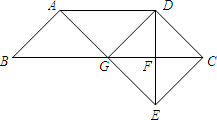 (2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G.
(2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G. 已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.
已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.