题目内容
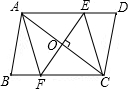 已知:如图,平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别交于F、F.
已知:如图,平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别交于F、F.(1)求证:四边形AFCE是菱形;
(2)如果BF比AE长2,BE=5,求sin∠FBE的值.
分析:(1)根据EF是对角线AC的垂直平分线,可以求证△AOE≌△COF,证明四边形的对角线互相平分,垂直,就可以证出.
(2)在直角△OFC中根据勾股定理就可以求出.
(2)在直角△OFC中根据勾股定理就可以求出.
解答:解:(1)∵EF是对角线AC的垂直平分线,
∴OA=OC,AC⊥EF,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAO=∠FCO,
∵∠AOE=∠COF,
∴在△AOE和△COF中,
∴△AOE≌△COF(ASA).
∴OE=OF.
∴四边形AFCE是平行四边形,
又∵AC⊥EF,
∴四边形是AFCE菱形.(1分)
(2)连接AE交BF于O点
,(2分)
∴
.(1分)
在Rt△BOE中,sin∠FBE=
=
.(2分)
∴OA=OC,AC⊥EF,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAO=∠FCO,
∵∠AOE=∠COF,
∴在△AOE和△COF中,
|
∴△AOE≌△COF(ASA).
∴OE=OF.
∴四边形AFCE是平行四边形,
又∵AC⊥EF,
∴四边形是AFCE菱形.(1分)
(2)连接AE交BF于O点
|
∴
|
在Rt△BOE中,sin∠FBE=
| OE |
| BE |
| 3 |
| 5 |
点评:本题主要考查了菱形的证明方法,以及平行四边形的性质,中心对称性.

练习册系列答案
相关题目




