题目内容
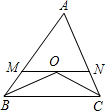 如图,OB、OC分别平分∠ABC与∠ACB,MN∥BC,若AB=24,AC=36,则△AMN的周长是
如图,OB、OC分别平分∠ABC与∠ACB,MN∥BC,若AB=24,AC=36,则△AMN的周长是60
60
.分析:根据角平分线的定义可得∠ABO=∠OBC,再根据两直线平行,内错角相等可得∠OBC=BOM,从而得到∠ABO=∠BOM,根据等角对等边的性质可得BM=OM,同理可得CN=ON,然后求出△AMN的周长=AB+AC,代入数据进行计算即可得解.
解答:解:∵OB平分∠ABC,
∴∠ABO=∠OBC,
∵MN∥BC,
∴∠OBC=BOM,
∴∠ABO=∠BOM,
∴BM=OM,
同理可得CN=ON,
∴△AMN的周长=AM+MO+ON+AN=AM+BM+CN+AN=AB+AC,
∵AB=24,AC=36,
∴△AMN的周长=24+36=60.
故答案为:60.
∴∠ABO=∠OBC,
∵MN∥BC,
∴∠OBC=BOM,
∴∠ABO=∠BOM,
∴BM=OM,
同理可得CN=ON,
∴△AMN的周长=AM+MO+ON+AN=AM+BM+CN+AN=AB+AC,
∵AB=24,AC=36,
∴△AMN的周长=24+36=60.
故答案为:60.
点评:本题考查了等腰三角形的判定与性质,主要利用了等角对等边的性质,两直线平行,内错角相等的性质,是基础题,熟记性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图,OB、OC分别为∠ABC,∠ACB的平分线,∠BOC随着∠A的变化而变化.为探究∠A和∠BOC的关系,现采取如下两种方案,在变化过程中,设∠A为x°,∠BOC为y°.
方案甲:用量角器量出∠A、∠BOC的不断变化时的具体数据,并列表如下: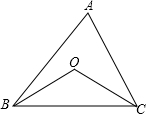
建立直角坐标系,并描点、连线,猜测y与x之间的函数关系,求出y与x的函数关系式.
方案乙:利用角平分线的性质及三角形内角和为180°的性质,直接进行计算,求出y与x之间的函数关系.
(1)若x=60°,则y= .(请直接写 出结果)
出结果)
(2)请采用方案甲或方案乙中的一种进行解答,得到∠A与∠BOC之间的关系.
方案甲:用量角器量出∠A、∠BOC的不断变化时的具体数据,并列表如下:

| x | 10 | 20 | 30 | 40 | … |
| y | 95 | 100 | 105 | 110 | … |
方案乙:利用角平分线的性质及三角形内角和为180°的性质,直接进行计算,求出y与x之间的函数关系.
(1)若x=60°,则y=
 出结果)
出结果)(2)请采用方案甲或方案乙中的一种进行解答,得到∠A与∠BOC之间的关系.
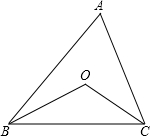 如图,OB、OC分别平分∠ABC和∠ACB,若∠A=60°,则∠O等于( )
如图,OB、OC分别平分∠ABC和∠ACB,若∠A=60°,则∠O等于( )| A、100° | B、120° | C、140° | D、150° |
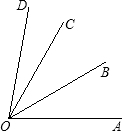 已知:如图,OB、OC分别为定角∠AOD内的两条动射线
已知:如图,OB、OC分别为定角∠AOD内的两条动射线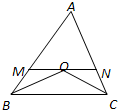 3、如图,OB,OC分别平分∠ABC与∠ACB,MN∥BC,若AB=24,AC=36,则△AMN的周长是( )
3、如图,OB,OC分别平分∠ABC与∠ACB,MN∥BC,若AB=24,AC=36,则△AMN的周长是( )