Question

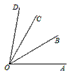
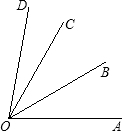已知：如图，OB、OC分别为定角∠AOD内的两条动射线
（1）当OB、OC运动到如图的位置时，∠AOC+∠BOD=110°，∠AOB+∠COD=50°，求∠AOD的度数；
（2）在（1）的条件下，射线OM、ON分别为∠AOB、∠COD的平分线，当∠COB绕着点O旋转时，下列结论：①∠AOM-∠DON的值不变；②∠MON的度数不变．可以证明，只有一个是正确的，请你作出正确的选择并求值．

Answer 1

分析：（1）根据角的定义可知∠AOC+∠BOD=∠AOB+∠COD+2∠BOC，根据题意得出2∠BOC+50°=110°，求出∠BOC的度数，即可求出∠AOD的度数，
（2）根据角平分线的定义得出∠MON=∠CON+∠BOM+∠BOC=25°+30°=55°．

解答：解：（1）∵∠AOC+∠BOD=∠AOB+∠COD+2∠BOC，
∠AOC+∠BOD=110°，∠AOB+∠COD=50°，
∴110°=2∠BOC+50°，
∴∠BOC=30°，
∴∠AOD=∠BOC+∠AOB+∠COD=80°；

（2）②正确，∠MON=55°，
∵OM、ON分别为∠AOB、∠COD的平分线，
∴∠CON+∠BOM=

1

2

（∠AOB+∠COD）=25°，
∴∠MON=∠CON+∠BOM+∠BOC=25°+30°=55°．

点评：本题考查了角的计算以及角平分线的定义，须根据已知条件一步步计算，难度较大．