题目内容
【题目】在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:
如果矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形.例如,下图中的矩形A1B1C1D1 , A2B2C2D2 , AB3C3D3都是点A,B,C的覆盖矩形,其中矩形AB3C3D3是点A,B,C的最优覆盖矩形.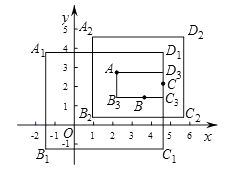
(1)已知A( ![]() 2,3),B(5,0),C(
2,3),B(5,0),C( ![]() ,
, ![]() 2).
2).
①当 ![]() 时,点A,B,C的最优覆盖矩形的面积为;
时,点A,B,C的最优覆盖矩形的面积为;
②若点A,B,C的最优覆盖矩形的面积为40,则t的值为;
(2)已知点D(1,1),点E( ![]() ,
, ![]() ),其中点E是函数
),其中点E是函数 ![]() 的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
【答案】
(1)35.;t=-3或6.
(2)
解:如图1,
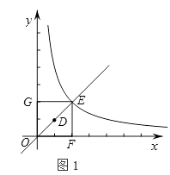
OD所在的直线交双曲线于点E,矩形OFEG是点O,D,E的一个面积最小的最优覆盖矩形,
∵点D(1,1),
∴OD所在的直线表达式为y=x,
∴点E的坐标为(2,2),
∴OE=![]() ,
,
∴⊙H的半径r =![]() .
.
如图2,
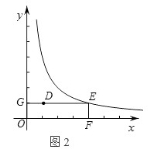
∵当点E的纵坐标为1时,1=![]() ,解得x=4,
,解得x=4,
∴OE=![]() ,
,
∴⊙H的半径r =![]() ,
,
∴![]()
![]() r
r![]()
![]() .
.
【解析】此题考查反比例函数图象和性质和圆的知识的综合应用,正确理解最优覆盖矩形定义是解题关键,综合性强,有一定难度.

练习册系列答案
相关题目