题目内容
若f(x)= ,则方程f(4x)=x的根是________.
,则方程f(4x)=x的根是________.

分析:由f(4x)=x建立方程,进行化简配方可解得方程的根.
解答:∵f(4x)=x,
∴
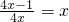 (x≠0)
(x≠0)化简,得4x2-4x+1=(2x-1)2=0,
解得
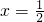 ,
,故答案为:
 .
.点评:本题考查了方程根的问题,属于基础问题,培养学生计算能力.

练习册系列答案
相关题目
题目内容
 ,则方程f(4x)=x的根是________.
,则方程f(4x)=x的根是________.
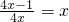 (x≠0)
(x≠0)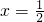 ,
, .
.