题目内容
【题目】如图,平面直角坐标系中,O为菱形ABCD的对称中心,已知C(2,0),D(0,﹣1),N为线段CD上一点(不与C、D重合).
(1)求以C为顶点,且经过点D的抛物线解析式;
(2)设N关于BD的对称点为N1 , N关于BC的对称点为N2 , 求证:△N1BN2∽△ABC;
(3)求(2)中N1N2的最小值;
(4)过点N作y轴的平行线交(1)中的抛物线于点P,点Q为直线AB上的一个动点,且∠PQA=∠BAC,求当PQ最小时点Q坐标.
【答案】
(1)解:由已知,设抛物线解析式为y=a(x﹣2)2
把D(0,﹣1)代入,得a=﹣ ![]()
∴y=﹣ ![]() (x﹣2)2
(x﹣2)2
(2)解:如图1,连结BN.
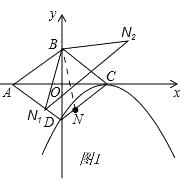
∵N1,N2是N的对称点
∴BN1=BN2=BN,∠N1BD=∠NBD,∠NBC=∠N2BC
∴∠N1BN2=2∠DBC
∵四边形ABCD是菱形
∴AB=BC,∠ABC=2∠DBC
∴∠ABC=∠N1BN2, ![]()
∴△ABC∽△N1BN2
(3)解:∵点N是CD上的动点,
∴点到直线的距离,垂线段最短,
∴当BN⊥CD时,BN最短.
∵C(2,0),D(0,﹣1)
∴CD= ![]() ,
,
∴BNmin= ![]() ,
,
∴BN1min=BNmin= ![]() ,
,
∵△ABC∽△N1BN2
∴ ![]() ,
,
N1N2min= ![]()
(4)解:如图2,
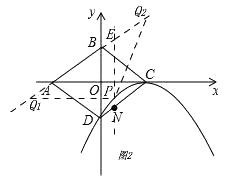
过点P作PE⊥x轴,交AB于点E.
∵∠PQA=∠BAC
∴PQ1∥AC
∵菱形ABCD中,C(2,0),D(0,﹣1)
∴A(﹣2,0),B(0,1)
∴lAB:Y= ![]() x+1
x+1
不妨设P(m,﹣ ![]() (m﹣2)2),则E(m,
(m﹣2)2),则E(m, ![]() m+1)
m+1)
∴PE= ![]() m2﹣
m2﹣ ![]() m+2
m+2
∴当m=1时, ![]()
此时,PQ1最小,最小值为 ![]() =
= ![]() ,
,
∴PQ1=PQ2= ![]()
【解析】(1)由抛物线顶点在x轴上,可得抛物线可设为y=a(x-h)2再由顶点坐标C(2,0),点D(0,﹣1)利用待定系数法易得解析式为y=﹣![]() (x﹣2)2。
(x﹣2)2。
(2)由对称易得BN1=BN2=BN,又AB=BC可得对应边成比例,又由对称易得∠ABC=∠N1BN2可证△ABC∽△N1BN2。
(3)由(2)△ABC∽△N1BN2,由于三边比不变,所以BN1最小时,可得N1N2最小;由点与直线之间,垂线段最短,易得BN1⊥AD时最短,所以最后得证N1N2最小值。
(4)由所给条件∠PQA=∠BAC可得PQ1∥AC又已知菱形ABCD中,C(2,0),D(0,﹣1)可得A(﹣2,0),B(0,1)得到直线AB的解析式lAB:Y= ![]() x+1;若设P(m,﹣
x+1;若设P(m,﹣ ![]() (m﹣2)2),则可由点Q为直线AB上的一个动点得E(m,
(m﹣2)2),则可由点Q为直线AB上的一个动点得E(m, ![]() m+1),则PE为纵坐标的差PE=
m+1),则PE为纵坐标的差PE= ![]() m2﹣
m2﹣ ![]() m+2;此时PQ1最小,易由三角函数可得PQ1=PQ2=
m+2;此时PQ1最小,易由三角函数可得PQ1=PQ2= ![]()
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.





