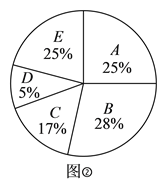题目内容
【题目】作图题：（不写作法，但要保留痕迹）
如图1，已知点C、D和∠AOB，求作一点P，使P到点C、D的距离相等，且到∠AOB的两边的距离相等．在图2中直线m上找到一点Q，使它到A、B两点的距离和最小．
【答案】解：如图1，点P即为所求；
如图2，点Q即为所求．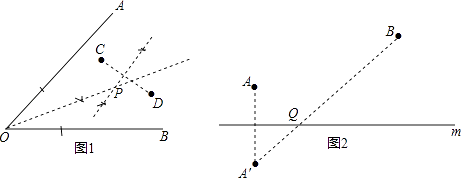
【解析】连接CD，作线段CD的垂直平分线与∠AOB的平分线，两直线的交点即为P点；作点A关于直线l的对称点A′，再连接A′B交直线l于点Q，则点Q即为所求．
【考点精析】认真审题，首先需要了解角平分线的性质定理(定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上)，还要掌握线段垂直平分线的性质(垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等)的相关知识才是答题的关键．
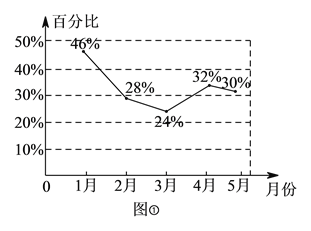
【题目】某商场去年前五个月销售额共计
万元．下表表示该商场去年前五个月的月销售额（统计信息不全）．图①表示该商场服装部各月销售额占商场当月销售额的百分比情况统计图．
商场月销售额统计表
单位：万元
月份 |
|
|
|
|
|
商场月销售额 |
|
|
|
|
服装部各月销售额占市场 当月销售额的百分比统计图 |
占 |
|
|
（
）商场
月份的销售额是__________万元．
（
）服装部
月份的销售额是__________万元．
小明同学观察图①后认为，服装部月份的销售额比服装部
月份的销售额减少了，你同意他的看法吗？请说明理由．
答：__________．
（
）在该商场服装部，下设
、
、
、
、
五个卖区，图②表示在月份，服装部各卖区销售额占月份服装部销售额的百分比情况统计图．则__________卖区的销售额最高，销售额最高的卖区占月份商场销售额的百分比是__________．
