题目内容
【题目】用火柴棒按下列方式搭建三角形:
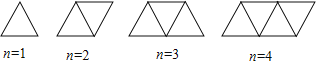
(1)当三角形个数为1时,需3根火柴棒;当三角形个数为2时,需5根火柴棒;则当三角形个数为100时,需火柴棒 根;当三角形个数为n时,需火柴棒 根(用含n的代数式表示);
(2)当火柴棒的根数为2019时,求三角形的个数?
(3)组成三角形的火柴棒能否为1000根,如果能,求三角形的个数;如果不能,请说明理由.
【答案】(1)201;(2n+1);(2)1009;(3)组不能为1000根,理由见解析
【解析】
(1)根据题目中的图形,可以发现火柴棒根数的变化规律,从而可以得到当三角形个数为100时,需火柴棒的根数和当三角形个数为n时,需火柴棒的根数;
(2)根据(1)中的结果,可以求得当火柴棒的根数为2019时,三角形的个数;
(3)根据(1)中的结果,可以说明组成三角形的火柴棒能否为1000根.
解:(1)由图可得,
当n=1时,火柴棒的根数为:1+2×1=3,
当n=2时,火柴棒的根数为:1+2×2=5,
当n=3时,火柴棒的根数为:1+2×3=7,
当n=4时,火柴棒的根数为:1+2×4=9,
…,
当n=100时,火柴棒的根数为:1+2×100=201,
当三角形个数为n时,需火柴棒的根数为:1+2×n=2n+1,
故答案为:201,(2n+1);
(2)令2n+1=2019,得n=1009,
即当火柴棒的根数为2019时,三角形的个数是1009;
(3)令1+2n=1000,得n=499.5不是整数,
故组成三角形的火柴棒不能为1000根.

练习册系列答案
相关题目