Question

复习“全等三角形”的知识时，老师布置了一道作业题：“如下图①，已知在△ABC中，AB＝AC，P是△ABC内部任意一点，将AP绕A顺时针旋转至AQ，使得∠QAP＝∠BAC，连接BQ、CP，则BQ＝CP。”

           

（1）小亮是个爱动脑筋的同学，他通过对图①的分析，证明了△ABQ≌△ACP，从而证得BQ＝CP。请你帮小亮完成证明。

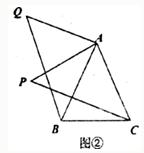
（2）之后，小亮又将点P移到等腰三角形ABC之外，原题中的条件不变，“BQ＝CP”仍然成立吗？若成立，请你就图②给出证明。若不成立，请说明理由。

Answer 1

证明：（1）∵∠QAP＝∠BAC

∴∠QAP－∠BAP＝∠BAC－∠BAP

即∠QAB＝∠CAP               

在△BQA和△CPA中

AP＝AQ，∠QAB＝∠CAP，AB＝AC

∴△BQA≌△CPA（SAS）    

∴BQ＝CP                 

（2）BQ＝CP仍然成立，理由如下：   

∵∠QAP＝∠BAC

∴∠QAP＋∠PAB＝∠BAC＋∠PAB     

即∠QAB＝∠PAC

在△QAB和△PAC中

AP＝AQ，∠QAB＝∠PAC，AB＝AC

∴△QAB≌△PAC（SAS）    

∴BQ＝CP