题目内容
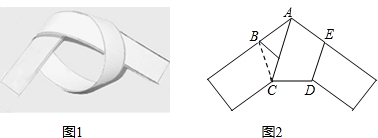
用一条宽相等的足够长的纸条,打一个结,如图1所示,然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE,则S△ABC:S四边形ACDE的值为( )

| A、1:2 | ||
| B、1:3 | ||
C、(
| ||
D、(3-
|
分析:连接BD、CE,由于ABCDE是正五边形,那么首先求出∠BAC、∠BCA的度数,易知△ABC、△CDE的面积相等,因此只需比较△ABC、△ACE的面积即可;易得AB∥CE,那么△ABC、△ACE同高,则面积比等于底边的比,上面求得了∠ACE=∠BAC=36°,那么CE、AE的比例关系即可得出,进而求得△ABC与△ACE的面积比,也就得到了△ABC、四边形ACDE的面积比.
解答: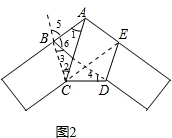 解:如图;
解:如图;
由折叠的性质知:∠5=∠6;
∵正五边形ABCDE中,∠1=∠2=∠3=∠4,
∴设∠1=α,则∠5=∠6=2α;
则在△ABC中:α+α+α+2α=180°,即∠1=α=36°;
同理,∠ACE=∠1=36°,
则AB∥CE,且CE=
AE;
∴S△AEC:S△ABC=CE:AE=CE:AB=
:1;
设S△ABC=1,则S△CDE=S△ABC=1,S△AEC=
,S四边形ACDE=S△ACE+S△CDE=
;
所以S△ABC:S四边形ACDE=1:
=(3-
):2,
故选D.
 解:如图;
解:如图;由折叠的性质知:∠5=∠6;
∵正五边形ABCDE中,∠1=∠2=∠3=∠4,
∴设∠1=α,则∠5=∠6=2α;
则在△ABC中:α+α+α+2α=180°,即∠1=α=36°;
同理,∠ACE=∠1=36°,
则AB∥CE,且CE=
1+
| ||
| 2 |
∴S△AEC:S△ABC=CE:AE=CE:AB=
1+
| ||
| 2 |
设S△ABC=1,则S△CDE=S△ABC=1,S△AEC=
1+
| ||
| 2 |
3+
| ||
| 2 |
所以S△ABC:S四边形ACDE=1:
3+
| ||
| 2 |
| 5 |
故选D.
点评:此题主要考查了图形的翻折变换,以及图形面积的求法;要注意的是顶角为36°的等腰三角形所含的特殊意义.

练习册系列答案
相关题目
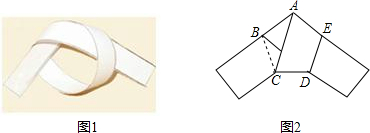
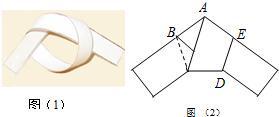
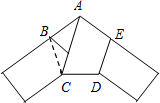 用一条宽相等的足够长的纸条,打一个结,然后拉紧、压平就可以得到如图所示的正五边形ABCDE,其中∠CAE度数( )
用一条宽相等的足够长的纸条,打一个结,然后拉紧、压平就可以得到如图所示的正五边形ABCDE,其中∠CAE度数( )
