Question

【题目】已知：如图①，在矩形ABCD中，AB＝5，AD＝．E为矩形外一点，且△EBA∽△ABD．

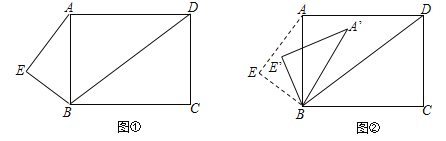
(1)、求AE和BE的长；

(2)、若将△ABE沿着射线BD方向平移，设平移的距离为m（平移距离指点B沿BD方向所经过的线段长度）．当点E分别平移到线段AB、AD上时，直接写出相应的m的值；

(3)、如图②，将△ABE绕点B顺时针旋转一个角α（0°＜α＜180°），记旋转中的△ABE为△A′BE′，在旋转过程中，设A′E′所在的直线与直线AD交于点P，与直线BD交于点Q．是否存在这样的P、Q两点，使△DPQ为等腰三角形？若存在，求出此时DQ的长；若不存在，请说明理由．

Answer 1

【答案】(1)、AE＝4，BE＝3；(2)、m=3；m=；(3)、DQ=3－、、－或.

【解析】

试题分析：(1)、根据三角形相似得出AE和BE的长度；(2)、分两种情况分别计算出m的值；(3)、分四种情况分别求出DQ的长度.

试题解析：(1)、AE＝4，BE＝3

(2)、点E在AB上时，m＝3；点E在AD上时，m=

(3)、存在．理由如下：在旋转过程中，等腰△DPQ依次有以下4种情形：

①如图3﹣1所示，点Q落在BD延长线上，且PD＝DQ，求得DQ=3－；

②如图3﹣2所示，点Q落在BD上，且PQ＝DQ，求得DQ=；

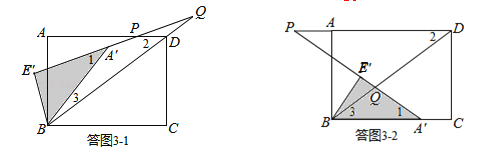
③如图3﹣3所示，点Q落在BD上，且PD＝DQ，求得DQ=－；

④如图3﹣4所示，点Q落在BD上，且PQ＝PD，求得DQ=．

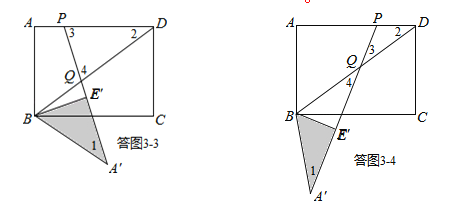
综上所述，存在4组符合条件的点P、点Q，使△DPQ为等腰三角形：

DQ的长度分别为3－、、－或.