Question

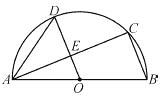
【题目】如图，在△ABC中，∠ACB＝90°，AC＝BC，△ABC的高CD与角平分线AE相交点F，过点C作CH⊥AE于G，交AB于H．

（1）求∠BCH的度数；

（2）求证：CE＝BH．

Answer 1

【答案】(1)22.5°；（2）见解析．

【解析】试题分析：（1）根据AE是角平分线，可得∠ACE的度数，再根据直角三角形两余角互余可得∠AEC的度数，再由CH⊥AE即可得；

（2）证明CF=CE，再证明△ACF≌△CBH即可得.

试题解析：（1）∵∠ACB＝90°，AC＝BC，

∴∠CAB＝∠B＝45°，

∵AE是△ABC的角平分线，

∴∠CAE＝∠CAB＝22.5°，

∴∠AEC＝90°-∠CAE＝67.5°，

∵CH⊥AE于G，

∴∠CGE＝90°，

∴∠GCE＝90°-∠AEC＝22.5°；

（2）∵∠ACB＝90°，AC＝BC，CD是△ABC的高，

∴∠ACD＝∠ACB＝45°，

∴∠CFE＝∠CAE＋∠ACD＝67.5°，

∴∠CFE＝∠AEC，

∴CF＝CE，

在△ACF和△CBH中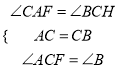，∴△ACF≌△CBH，∴CF＝BH，

∴CE＝BH.