题目内容
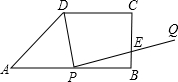
如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,在AB边上取动点P,连接DP,作PQ⊥DP,使得PQ交射线BC于点E,设AP=x,BE=y.
(1)当BC=4时,试写出y关于x的函数关系式;
(2)在满足(1)的条件下,若△APD是等腰三角形时,求BE的长;
(3)在满足(1)的条件下,点E能否与C点重合?若存在,求出相应的AP的长;若不存在,请说明理由;
(4)当BC在什么范围内,存在点P,使得PQ经过C(直接写出结果).
解:(1)过D点作DH⊥AB于H,
则四边形DHBC为矩形,
∴HB=CD=6,∴AH=AB-CD=2.
∵AP=x,∴PH=x-2,
∵∠DPH+∠PDH=90°,∠DPH+∠BPE=90°,
∴∠PDH=∠BPE.
∵∠DHP=∠B=90°,
∴△DPH∽△PEB.
∴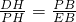 ,∴
,∴ ,
,
整理得:y= (x-2)(8-x)=-
(x-2)(8-x)=- x2+
x2+ x-4,
x-4,
∵在AB边上取动点P,连接DP,作PQ⊥DP,使得PQ交射线BC于点E,AH=2,
∴2<x<6,
即y=- x2+
x2+ x-4(2<x<8);
x-4(2<x<8);
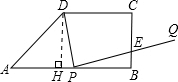
(2)直角三角形AHD中,AH=AB-CD=2,DH=BC=4,根据勾股定理可得:AD=2 ,
,
要使△APD是等腰三角形,则
情况①:当AP=AD=2 ,即x=2
,即x=2 时:
时:
BE=y=- ×(2
×(2 )2+
)2+ ×2
×2 -4=5
-4=5 -9
-9
情况②:当AD=PD时,则AH=PH,
∵AH=2,PH=x-2,∴2=x-2,解得x=4,符合x的取值范围,
那么:BE=y=- ×42+
×42+ ×4-4=2
×4-4=2
情况③:当AP=PD时,则AP2=PD2,
∴x2=42+(x-2)2,解得x=5,符合x的取值范围,
那么:BE=y=- ×52+
×52+ ×5-4=2
×5-4=2
(3)在满足(1)的条件下,若存在点E能与C点重合,
则y=- x2+
x2+ x-4=4,整理得:x2-10x+32=0
x-4=4,整理得:x2-10x+32=0
∵△=(-10)2-4×32<0,∴原方程无实数解,
∴在满足(1)的条件下,不存在点E与C点重合.
(4)在满足0<BC≤ 时,存在点P,使得PQ经过C.
时,存在点P,使得PQ经过C.
分析:(1)可通过构建相似三角形来求解,过D作AB的垂线DH,垂足为H,那么根据AB、CD的长,就能表示出AH、BH、PH的长,然后通过证三角形DPH和PBE相似,得出关于DH、PH、PB、BE的比例关系式,由于BC=DH,因此可得出关于x、y函数关系式.
(2)可分三种情况进行讨论;
①当AP=AD时,AD可在直角三角形ADH中,根据AH的长和BC的长用勾股定理得出.那么此时就得出了AP的值即x的值,然后代入(1)的函数式即可得出BE的长.
②当AD=PD时,可根据等腰三角形三线合一的特点先求出AH的值,那么AH=PH即可得出x的值,然后代入(1)的函数式求出BE.
③当AP=PD时,可在直角三角形DPH中用含x的式子表示出PD2,然后根据AP2=AD2,求出x的值,然后根据(1)的函数式求出BE的长.
(3)当E与C重合时,BE=AH,然后将(1)中得出的AH的值,代入(1)的函数式中,可得出一个关于x的二元一次方程,那么看看这个方程是否有解即可判断出是否存在E与C重合的情况.
(4)如果在运动的过程中,始终保持∠DPC=90°,那么以DC为直径的圆会与AB相交或相切,为此DC的中点即圆心到AB的距离会小于等于半径3.那么BC应满足的条件应该是0<BC≤ .
.
点评:本题主要考查了直角梯形的性质,相似三角形的判定和性质以及二次函数的综合应用等知识点,通过构建相似三角形来得出二次函数是解题的关键.
则四边形DHBC为矩形,
∴HB=CD=6,∴AH=AB-CD=2.
∵AP=x,∴PH=x-2,
∵∠DPH+∠PDH=90°,∠DPH+∠BPE=90°,
∴∠PDH=∠BPE.
∵∠DHP=∠B=90°,
∴△DPH∽△PEB.
∴
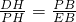 ,∴
,∴ ,
,整理得:y=
 (x-2)(8-x)=-
(x-2)(8-x)=- x2+
x2+ x-4,
x-4,∵在AB边上取动点P,连接DP,作PQ⊥DP,使得PQ交射线BC于点E,AH=2,
∴2<x<6,
即y=-
 x2+
x2+ x-4(2<x<8);
x-4(2<x<8);
(2)直角三角形AHD中,AH=AB-CD=2,DH=BC=4,根据勾股定理可得:AD=2
 ,
,要使△APD是等腰三角形,则
情况①:当AP=AD=2
 ,即x=2
,即x=2 时:
时:BE=y=-
 ×(2
×(2 )2+
)2+ ×2
×2 -4=5
-4=5 -9
-9情况②:当AD=PD时,则AH=PH,
∵AH=2,PH=x-2,∴2=x-2,解得x=4,符合x的取值范围,
那么:BE=y=-
 ×42+
×42+ ×4-4=2
×4-4=2情况③:当AP=PD时,则AP2=PD2,
∴x2=42+(x-2)2,解得x=5,符合x的取值范围,
那么:BE=y=-
 ×52+
×52+ ×5-4=2
×5-4=2
(3)在满足(1)的条件下,若存在点E能与C点重合,
则y=-
 x2+
x2+ x-4=4,整理得:x2-10x+32=0
x-4=4,整理得:x2-10x+32=0∵△=(-10)2-4×32<0,∴原方程无实数解,
∴在满足(1)的条件下,不存在点E与C点重合.
(4)在满足0<BC≤
 时,存在点P,使得PQ经过C.
时,存在点P,使得PQ经过C.分析:(1)可通过构建相似三角形来求解,过D作AB的垂线DH,垂足为H,那么根据AB、CD的长,就能表示出AH、BH、PH的长,然后通过证三角形DPH和PBE相似,得出关于DH、PH、PB、BE的比例关系式,由于BC=DH,因此可得出关于x、y函数关系式.
(2)可分三种情况进行讨论;
①当AP=AD时,AD可在直角三角形ADH中,根据AH的长和BC的长用勾股定理得出.那么此时就得出了AP的值即x的值,然后代入(1)的函数式即可得出BE的长.
②当AD=PD时,可根据等腰三角形三线合一的特点先求出AH的值,那么AH=PH即可得出x的值,然后代入(1)的函数式求出BE.
③当AP=PD时,可在直角三角形DPH中用含x的式子表示出PD2,然后根据AP2=AD2,求出x的值,然后根据(1)的函数式求出BE的长.
(3)当E与C重合时,BE=AH,然后将(1)中得出的AH的值,代入(1)的函数式中,可得出一个关于x的二元一次方程,那么看看这个方程是否有解即可判断出是否存在E与C重合的情况.
(4)如果在运动的过程中,始终保持∠DPC=90°,那么以DC为直径的圆会与AB相交或相切,为此DC的中点即圆心到AB的距离会小于等于半径3.那么BC应满足的条件应该是0<BC≤
 .
.点评:本题主要考查了直角梯形的性质,相似三角形的判定和性质以及二次函数的综合应用等知识点,通过构建相似三角形来得出二次函数是解题的关键.

练习册系列答案
相关题目
 已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )
已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )A、
| ||||
B、4
| ||||
C、
| ||||
D、4
|
 5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有
5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有 10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( )
10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( ) 如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,
如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2, 如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.
如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.