��Ŀ����
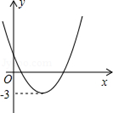
��ƽ��ֱ������ϵxOy�У���֪���κ��� ��ͼ����x��������ύ��A
��ͼ����x��������ύ��A ��B
��B ���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C ����A�͵�B��ľ���Ϊ2�� �������κ���
���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C ����A�͵�B��ľ���Ϊ2�� �������κ��� ��ͼ����y������ƽ��3����λʱ������ǡ�ù�ԭ�㣬����x���������ľ���Ϊ4��
��ͼ����y������ƽ��3����λʱ������ǡ�ù�ԭ�㣬����x���������ľ���Ϊ4��
��1������κ��� �ı���ʽ��
�ı���ʽ��
��2���ڶ��κ��� ��ͼ��ĶԳ������Ƿ����һ��P��ʹ��P��B��C�������֮����������ڣ������P���ꣻ�������ڣ���˵�����ɣ�
��ͼ��ĶԳ������Ƿ����һ��P��ʹ��P��B��C�������֮����������ڣ������P���ꣻ�������ڣ���˵�����ɣ�
��3������κ��� ��ͼ��Ķ���ΪD����x�����Ƿ���������ĵ�F��ʹ��
��ͼ��Ķ���ΪD����x�����Ƿ���������ĵ�F��ʹ�� �������ڣ������F�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ������F�����ꣻ�������ڣ���˵�����ɣ�
 ��ͼ����x��������ύ��A
��ͼ����x��������ύ��A ��B
��B ���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C ����A�͵�B��ľ���Ϊ2�� �������κ���
���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C ����A�͵�B��ľ���Ϊ2�� �������κ��� ��ͼ����y������ƽ��3����λʱ������ǡ�ù�ԭ�㣬����x���������ľ���Ϊ4��
��ͼ����y������ƽ��3����λʱ������ǡ�ù�ԭ�㣬����x���������ľ���Ϊ4����1������κ���
 �ı���ʽ��
�ı���ʽ�� ��2���ڶ��κ���
 ��ͼ��ĶԳ������Ƿ����һ��P��ʹ��P��B��C�������֮����������ڣ������P���ꣻ�������ڣ���˵�����ɣ�
��ͼ��ĶԳ������Ƿ����һ��P��ʹ��P��B��C�������֮����������ڣ������P���ꣻ�������ڣ���˵�����ɣ���3������κ���
 ��ͼ��Ķ���ΪD����x�����Ƿ���������ĵ�F��ʹ��
��ͼ��Ķ���ΪD����x�����Ƿ���������ĵ�F��ʹ�� �������ڣ������F�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ������F�����ꣻ�������ڣ���˵�����ɣ���1�� ����2�����ڣ���2��3������3�����ڣ���-1��0����5��0����
����2�����ڣ���2��3������3�����ڣ���-1��0����5��0����
 ����2�����ڣ���2��3������3�����ڣ���-1��0����5��0����
����2�����ڣ���2��3������3�����ڣ���-1��0����5��0���������������1������ƽ�Ƶ����ʣ��õ��Գ���У��Ӷ������A��B�����꣬Ӧ�ô���ϵ����������ö��κ���
 �ı���ʽ��
�ı���ʽ����2��������ԳƵ����ʣ�ֱ֪��AC��ֱ��x=2�Ľ���P���ǵ�B��C�������֮�����ĵ㣬������ֱ��AC�ķ��̣�������õ�P���꣮
��3������֤����BCD��ֱ�������β����BC��BD��ֵ���õ�
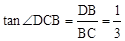 ���Ӷ�ֻҪ���ʹ
���Ӷ�ֻҪ���ʹ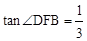 ʱ��F�����꼴�ɣ�
ʱ��F�����꼴�ɣ������������1����ƽ�ƺ�ĺ���ͼ���ԭ������x���������ľ���Ϊ4��
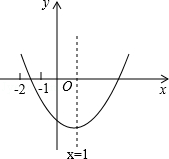
��ƽ�ƺ�ĺ���ͼ����x������������Ϊ��0��0��,(4,0)��0��0������-4��0����
�����ĶԳ���Ϊֱ��x=2��x=-2��
��������
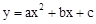 ��x��������ύ��A��B���㣬
��x��������ύ��A��B���㣬��������
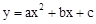 ����ֱ��x=2�Գƣ�
����ֱ��x=2�Գƣ�������x���������ľ���Ϊ2���ҵ�A �ڵ�B����࣬
����ͼ����x�������������ΪA��1��0����B(3,0)��
������֪�����κ���
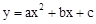 ��ͼ���C��0��-3����
��ͼ���C��0��-3��������
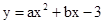 ��
����
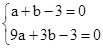 �����
�����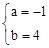 ��
������κ����ı���ʽΪ
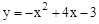 ��
����2���ߵ�B����ֱ��x=2�ĶԳƵ�ΪA��1��0����
��ֱ��AC�Ľ���ʽΪ
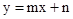 ��
����
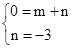 �����
�����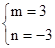 ��
����ֱ��AC�Ľ���ʽΪ
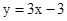 ��
��ֱ��AC��ֱ��x=2�Ľ���P���ǵ�B��C�������֮�����ĵ㣮
�ߵ�x=2ʱ��y=3�����P������Ϊ��2��3�� ��
��3����x���ϴ��������ĵ�F��ʹ��
 �� �������£�
�� �������£�������
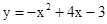 �Ķ���D������Ϊ��2��1����
�Ķ���D������Ϊ��2��1������Գ�����x��Ľ���Ϊ��E��
��
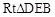 ����
����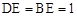 ����
����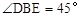 ��
����
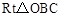 ����
���� ����
���� ��
����
 ��
����
 ����
����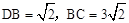 ����
����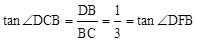 ��
����
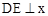 �ᣬ
�ᣬ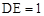 ����
����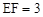 ��
����E��2��0����
���������ĵ�F������ΪF1��-1��0����F2��5��0����


��ϰ��ϵ�д�
�����Ŀ
 ��
�� �ύ�ڵ�A��B����y�ύ�ڵ�C�����е�B������Ϊ
�ύ�ڵ�A��B����y�ύ�ڵ�C�����е�B������Ϊ .
. ��B�Ķ�Ӧ��Ϊ
��B�Ķ�Ӧ��Ϊ ��C�Ķ�Ӧ��Ϊ
��C�Ķ�Ӧ��Ϊ ����ʹ�侭����2��������������G�Ķ���M������������G����һ������N�����
����ʹ�侭����2��������������G�Ķ���M������������G����һ������N����� �ľ���
�ľ��� ��ȡֵ��Χ.
��ȡֵ��Χ.
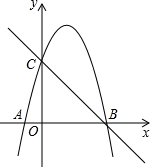
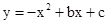 ����A
����A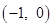 ��C��0��4�����㣬��x�����һ������B��
��C��0��4�����㣬��x�����һ������B��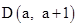 �ڵ�һ�����������ϣ����D����ֱ��BC�ĶԳƵ�
�ڵ�һ�����������ϣ����D����ֱ��BC�ĶԳƵ�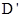 �����ꣻ
�����ꣻ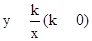 ��ͼ����E����
��ͼ����E����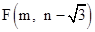 �ڴ˷���������ͼ���ϣ���
�ڴ˷���������ͼ���ϣ���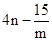 ��ֵ��
��ֵ��
 x2+bx+c������B���ҶԳ�����ֱ��x=��
x2+bx+c������B���ҶԳ�����ֱ��x=��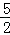 ��
�� ��
�� �����Գ�����ֱ��x=��
�����Գ�����ֱ��x=��